Lời giải
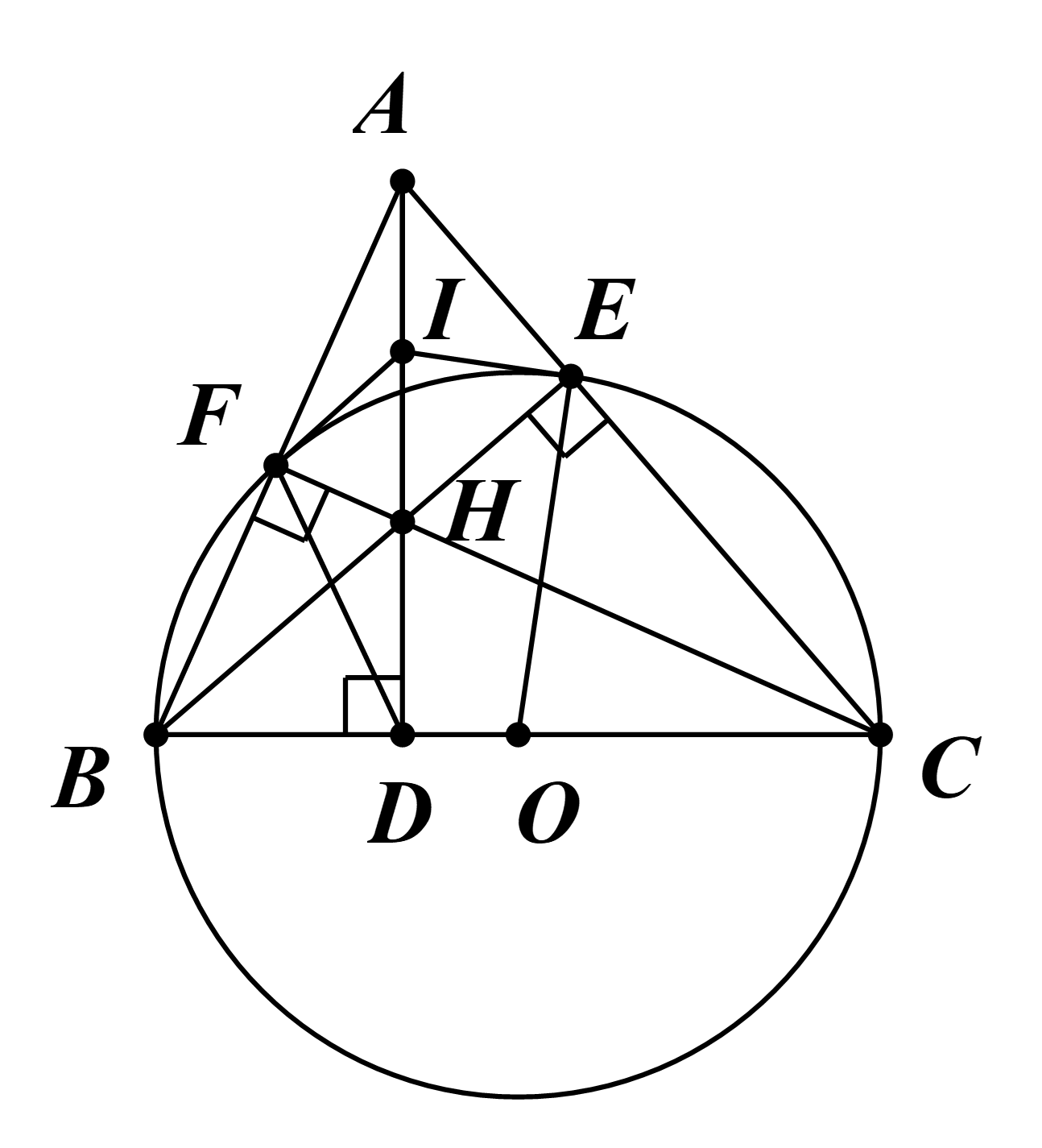
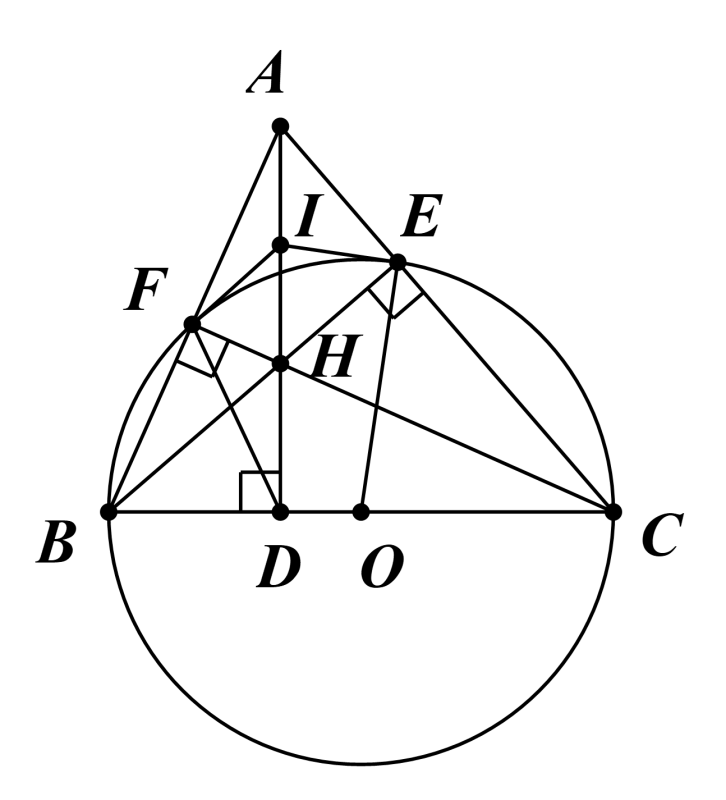
a) ∆BCF nội tiếp đường tròn tâm O, đường kính BC.
Suy ra (widehat {BFC}) là góc nội tiếp chắn nửa đường tròn đường kính BC.
Khi đó (widehat {BFC} = 90^circ ) hay (widehat {AFH} = 90^circ ).
Vì vậy ba điểm A, F, H cùng thuộc đường tròn đường kính AH (1)
Chứng minh tương tự, ta được (widehat {AEH} = 90^circ ).
Suy ra ba điểm A, E, H cùng thuộc đường tròn đường kính AH (2)
Từ (1), (2), ta được tứ giác AEHF nội tiếp đường tròn đường kính AH.
b) Ta có (widehat {FIE} = 2widehat {FAE} = 2.60^circ = 120^circ ) (góc nội tiếp bằng một nửa số đo của của bị chắn).
Suy ra .
Ta có I là tâm đường tròn ngoại tiếp tứ giác AEHF (giả thiết).
Suy ra I là trung điểm AH.
Do đó (IA = IH = frac{{AH}}{2} = frac{4}{2} = 2,,left( {cm} right)).
Diện tích hình quạt IEHF của đường tròn (I) là:
(S = frac{{pi .I{A^2}.n^circ }}{{360^circ }} = frac{{pi {{.2}^2}.120^circ }}{{360^circ }} = frac{{4pi }}{3},,,left( {c{m^2}} right)).
Vậy sđ và diện tích hình quạt IEHF của đường tròn (I) bằng (frac{{4pi }}{3},,c{m^2}).
c) ∆ABC có hai đường cao CF và BE cắt nhau tại H.
Suy ra H là trực tâm của ∆ABC.
Mà AH cắt BC tại D.
Do đó AD ⊥ BC.
Suy ra (widehat {HDB} = 90^circ ).
Khi đó ba điểm B, D, H cùng thuộc đường tròn đường kính BH (3)
Lại có (widehat {BFH} = 90^circ ) (chứng minh trên).
Suy ra ba điểm B, F, H cùng thuộc đường tròn đường kính BH (4)
Từ (3), (4), suy ra tứ giác BDHF nội tiếp đường tròn đường kính BH.
Do đó (widehat {HFD} = widehat {HBD}) (cùng chắn ) (*)
Ta có tứ giác AEHF nội tiếp đường tròn đường kính AH (chứng minh trên).
Suy ra (widehat {EFH} = widehat {EAH}) (cùng chắn ) (**)
Ta có (widehat {EBC} = widehat {CAD}) (cùng phụ với (widehat {ACB})) (***)
Từ (*), (**), (***), suy ra (widehat {HFD} = widehat {EFH}).
Vậy FH là tia phân giác của (widehat {DFE}).
d) Ta có tứ giác AEHF nội tiếp đường tròn đường kính AH (chứng minh trên).
Suy ra IE = IH.
Do đó ∆IEH cân tại I.
Vì vậy (widehat {IEH} = widehat {IHE}) (5)
Lại có (widehat {BHD} = widehat {IHE}) (cặp góc đối đỉnh) (6)
Mà (widehat {BHD} = widehat {ECO}) (cùng phụ với (widehat {ABC})) (7)
Ta có tứ giác BCEF nội tiếp đường tròn tâm O, đường kính BC (giả thiết).
Suy ra OE = OC.
Do đó ∆OEC cân tại O.
Vì vậy (widehat {ECO} = widehat {OEC}) (8)
Từ (5), (6), (7), (8), suy ra (widehat {IEH} = widehat {OEC}).
Mà (widehat {OEH} + widehat {OEC} = 90^circ ) (do BE ⊥ AC).
Suy ra (widehat {OEH} + widehat {IEH} = 90^circ ).
Do đó (widehat {IEO} = 90^circ ).
Vì vậy OE ⊥ EI.
Suy ra IE là tiếp tuyến của (O).
Chứng minh tương tự, ta được IF là tiếp tuyến của (O).
Mà I ∈ AH.
Vậy 2 tiếp tuyến của (O) tại E, F và AH đồng quy tại điểm I.