Trong thế giới hình học Euclid, tam giác là một trong những hình cơ bản và quan trọng nhất, ẩn chứa vô vàn định lý và công thức thú vị. Một trong số đó là công thức tính đường trung tuyến, một khái niệm không chỉ giúp chúng ta xác định độ dài của đường trung tuyến mà còn mở ra cánh cửa để giải quyết nhiều bài toán phức tạp. Việc hiểu rõ và chứng minh công thức tính đường trung tuyến không chỉ củng cố kiến thức nền tảng về hình học mà còn rèn luyện tư duy logic, khả năng suy luận toán học. Bài viết này sẽ đi sâu vào định nghĩa, tính chất và đặc biệt là các phương pháp chứng minh chi tiết công thức này, giúp bạn đọc nắm vững kiến thức một cách toàn diện và sâu sắc. Để tìm hiểu thêm về các công thức và kiến thức toán học khác, bạn có thể truy cập lophoctichcuc.com.
Khái Niệm Đường Trung Tuyến và Các Tính Chất Cơ Bản Trong Tam Giác
Đường trung tuyến là một trong những yếu tố đặc trưng của tam giác, đóng vai trò quan trọng trong việc nghiên cứu các tính chất và cấu trúc của hình học phẳng. Để chứng minh công thức tính đường trung tuyến một cách hiệu quả, trước hết chúng ta cần hiểu rõ về định nghĩa và các đặc điểm cơ bản của nó.
Định Nghĩa Đường Trung Tuyến
Trong một tam giác, đường trung tuyến là đoạn thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện. Mỗi tam giác có ba đỉnh, do đó sẽ có ba đường trung tuyến. Ví dụ, trong tam giác ABC:
- Đường trung tuyến xuất phát từ đỉnh A là đoạn thẳng AM, với M là trung điểm của cạnh BC.
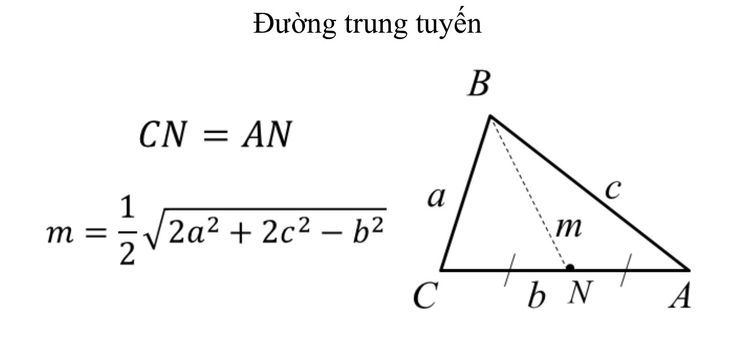
- Đường trung tuyến xuất phát từ đỉnh B là đoạn thẳng BN, với N là trung điểm của cạnh AC.
- Đường trung tuyến xuất phát từ đỉnh C là đoạn thẳng CP, với P là trung điểm của cạnh AB.
Các đường trung tuyến thường được ký hiệu là $m_a, m_b, m_c$ tương ứng với các cạnh đối diện là $a, b, c$.
Tính Chất Đồng Quy Của Các Đường Trung Tuyến
Một trong những tính chất nổi bật nhất của các đường trung tuyến trong tam giác là chúng đồng quy tại một điểm. Điểm đồng quy này được gọi là trọng tâm của tam giác, thường được ký hiệu là G. Trọng tâm G có một đặc điểm rất quan trọng: nó chia mỗi đường trung tuyến thành hai phần, trong đó phần gần đỉnh dài gấp đôi phần gần trung điểm của cạnh đối diện. Cụ thể, nếu AM là đường trung tuyến từ A đến BC, và G là trọng tâm, thì $AG = 2GM$ và $AM = 3GM$. Điều này cũng có nghĩa là $AG = frac{2}{3}AM$ và $GM = frac{1}{3}AM$.
Tính chất này không chỉ mang ý nghĩa lý thuyết mà còn có nhiều ứng dụng thực tiễn trong vật lý, đặc biệt là trong việc xác định tâm khối của các vật thể phẳng đồng chất có hình dạng tam giác. Trọng tâm chính là điểm cân bằng của tam giác.
Vai Trò Của Đường Trung Tuyến
Đường trung tuyến không chỉ là một khái niệm hình học đơn thuần mà còn là công cụ hữu ích để giải quyết các bài toán liên quan đến diện tích, chu vi, và các mối quan hệ giữa các cạnh và góc trong tam giác. Sự hiểu biết về đường trung tuyến là tiền đề để tiếp cận và chứng minh công thức tính đường trung tuyến, mở ra nhiều khám phá sâu hơn trong hình học.
Công Thức Tính Đường Trung Tuyến Trong Tam Giác
Sau khi đã nắm vững khái niệm và các tính chất cơ bản của đường trung tuyến, chúng ta sẽ đi vào công thức chính để tính độ dài của nó. Công thức này, còn được gọi là Định lý Apollonius, là nền tảng cho việc giải nhiều bài toán hình học và là trọng tâm của bài viết này khi chúng ta tìm cách chứng minh công thức tính đường trung tuyến.
Phát Biểu Công Thức
Cho một tam giác ABC với độ dài các cạnh là $a, b, c$. Gọi $m_a, m_b, m_c$ lần lượt là độ dài các đường trung tuyến xuất phát từ các đỉnh A, B, C tương ứng. Công thức tính độ dài đường trung tuyến $m_a$ (tức là đường trung tuyến đến cạnh a) là:
$m_a^2 = frac{2b^2 + 2c^2 – a^2}{4}$
Hoặc viết dưới dạng khai căn:
$m_a = frac{1}{2}sqrt{2b^2 + 2c^2 – a^2}$
Tương tự, ta có các công thức cho $m_b$ và $m_c$:
$m_b^2 = frac{2a^2 + 2c^2 – b^2}{4} implies m_b = frac{1}{2}sqrt{2a^2 + 2c^2 – b^2}$
$m_c^2 = frac{2a^2 + 2b^2 – c^2}{4} implies m_c = frac{1}{2}sqrt{2a^2 + 2b^2 – c^2}$
Giải Thích Các Biến Số
- $a, b, c$: Là độ dài các cạnh của tam giác ABC. Cạnh $a$ đối diện với đỉnh A, cạnh $b$ đối diện với đỉnh B, và cạnh $c$ đối diện với đỉnh C.
- $m_a$: Là độ dài đường trung tuyến xuất phát từ đỉnh A đến trung điểm của cạnh $a$ (cạnh BC).
- $m_b$: Là độ dài đường trung tuyến xuất phát từ đỉnh B đến trung điểm của cạnh $b$ (cạnh AC).
- $m_c$: Là độ dài đường trung tuyến xuất phát từ đỉnh C đến trung điểm của cạnh $c$ (cạnh AB).
Công thức này liên hệ độ dài của đường trung tuyến với độ dài các cạnh của tam giác, cung cấp một cách toán học để định lượng mối quan hệ hình học này. Việc nắm vững công thức này là bước đầu tiên để vận dụng nó vào giải quyết các bài toán, và việc hiểu sâu sắc nguồn gốc của nó thông qua các phương pháp chứng minh sẽ giúp ta ghi nhớ và áp dụng chính xác hơn.
Các Phương Pháp Chứng Minh Công Thức Tính Đường Trung Tuyến
Để chứng minh công thức tính đường trung tuyến một cách vững chắc, chúng ta có thể tiếp cận qua nhiều phương pháp khác nhau, mỗi phương pháp lại cung cấp một góc nhìn độc đáo và củng cố hiểu biết về các định lý hình học liên quan. Dưới đây là bốn phương pháp phổ biến và chi tiết. Tương tự như việc nắm vững [công thức bài toán chuyển động] để giải quyết các vấn đề vật lý, việc thành thạo công thức đường trung tuyến là chìa khóa để khai phá nhiều bài toán hình học phức tạp.
Phương Pháp 1: Sử Dụng Định Lý Cosin
Định lý Cosin là một trong những công cụ mạnh mẽ nhất trong hình học phẳng, giúp liên hệ độ dài các cạnh của một tam giác với cosin của một trong các góc của nó. Đây là phương pháp thường được sử dụng để chứng minh công thức tính đường trung tuyến.
Định lý Cosin: Trong một tam giác bất kỳ với các cạnh $x, y, z$ và góc $alpha$ đối diện với cạnh $x$, ta có: $x^2 = y^2 + z^2 – 2yz cos alpha$.
Các Bước Chứng Minh:
- Thiết lập: Xét tam giác ABC. Gọi AM là đường trung tuyến ứng với cạnh BC, với M là trung điểm của BC. Khi đó $BM = MC = frac{a}{2}$.
- Áp dụng Định lý Cosin cho tam giác ABM: Trong tam giác ABM, ta có cạnh $c = AB$, cạnh $m_a = AM$, cạnh $BM = frac{a}{2}$. Gọi $angle AMB = alpha$. Theo Định lý Cosin: $c^2 = m_a^2 + left(frac{a}{2}right)^2 – 2 cdot m_a cdot frac{a}{2} cdot cos alpha$ $c^2 = m_a^2 + frac{a^2}{4} – am_a cos alpha$ (Phương trình 1)
- Áp dụng Định lý Cosin cho tam giác ACM: Trong tam giác ACM, ta có cạnh $b = AC$, cạnh $m_a = AM$, cạnh $CM = frac{a}{2}$. Góc $angle AMC$ là góc bù với $angle AMB$, nên $angle AMC = 180^circ – alpha$. Do đó, $cos(angle AMC) = cos(180^circ – alpha) = -cos alpha$. Theo Định lý Cosin: $b^2 = m_a^2 + left(frac{a}{2}right)^2 – 2 cdot m_a cdot frac{a}{2} cdot cos(180^circ – alpha)$ $b^2 = m_a^2 + frac{a^2}{4} – am_a (-cos alpha)$ $b^2 = m_a^2 + frac{a^2}{4} + am_a cos alpha$ (Phương trình 2)
- Cộng hai phương trình: Cộng Phương trình 1 và Phương trình 2: $c^2 + b^2 = left(m_a^2 + frac{a^2}{4} – am_a cos alpharight) + left(m_a^2 + frac{a^2}{4} + am_a cos alpharight)$ $c^2 + b^2 = 2m_a^2 + 2frac{a^2}{4}$ $c^2 + b^2 = 2m_a^2 + frac{a^2}{2}$
- Rút gọn để tìm $m_a^2$: $2m_a^2 = c^2 + b^2 – frac{a^2}{2}$ $2m_a^2 = frac{2c^2 + 2b^2 – a^2}{2}$ $m_a^2 = frac{2c^2 + 2b^2 – a^2}{4}$
Đây chính là công thức cần chứng minh công thức tính đường trung tuyến. Phương pháp này trực quan và dễ hiểu, dựa trên một định lý cơ bản và quen thuộc.
Phương Pháp 2: Sử Dụng Định Lý Stewart (Mở Rộng)
Định lý Stewart là một định lý tổng quát hơn, áp dụng cho bất kỳ đoạn thẳng nào nối một đỉnh của tam giác với một điểm trên cạnh đối diện. Đường trung tuyến là một trường hợp đặc biệt của đoạn thẳng này.
Định lý Stewart: Cho tam giác ABC và một điểm D bất kỳ trên cạnh BC. Gọi $d = AD$, $m = BD$, $n = CD$, $a = BC$. Khi đó, định lý Stewart phát biểu rằng: $b^2m + c^2n = a(d^2 + mn)$
Các Bước Chứng Minh Công Thức Đường Trung Tuyến Bằng Định Lý Stewart:
- Áp dụng cho đường trung tuyến: Trong trường hợp đường trung tuyến AM, M là trung điểm của BC. Do đó, $BM = MC = frac{a}{2}$. Ta có $d = AM = m_a$, $m = BM = frac{a}{2}$, $n = CM = frac{a}{2}$.
- Thay thế vào công thức Stewart: $b^2 left(frac{a}{2}right) + c^2 left(frac{a}{2}right) = a left(m_a^2 + frac{a}{2} cdot frac{a}{2}right)$ $frac{a}{2} (b^2 + c^2) = a left(m_a^2 + frac{a^2}{4}right)$
- Rút gọn: Chia cả hai vế cho $a$ (vì $a ne 0$): $frac{1}{2} (b^2 + c^2) = m_a^2 + frac{a^2}{4}$
- Tìm $m_a^2$: $m_a^2 = frac{1}{2} (b^2 + c^2) – frac{a^2}{4}$ $m_a^2 = frac{2b^2 + 2c^2}{4} – frac{a^2}{4}$ $m_a^2 = frac{2b^2 + 2c^2 – a^2}{4}$
Phương pháp này thể hiện mối liên hệ chặt chẽ giữa đường trung tuyến và định lý Stewart tổng quát, giúp ta hiểu rõ hơn về tính chất của các đoạn thẳng trong tam giác.
Phương Pháp 3: Sử Dụng Vecto
Sử dụng vecto là một phương pháp mạnh mẽ trong hình học giải tích, cho phép chúng ta biến các bài toán hình học thành các phép toán đại số. Phương pháp này đòi hỏi một nền tảng về phép toán vecto. Để hiểu rõ hơn về các nguyên lý cơ bản trong vật lý, chẳng hạn như [công thức tính cường độ dòng điện qua bóng đèn], việc xây dựng nền tảng toán học vững chắc là điều thiết yếu.
Các Bước Chứng Minh:
- Chọn gốc tọa độ và biểu diễn vecto: Đặt gốc tọa độ tại A. Khi đó, $vec{A} = vec{0}$. Gọi $vec{B}$ và $vec{C}$ là các vecto vị trí của các đỉnh B và C. Điểm M là trung điểm của BC, nên $vec{M} = frac{vec{B} + vec{C}}{2}$. Đường trung tuyến AM có độ dài $m_a = |vec{AM}| = |vec{M} – vec{A}| = |vec{M}| = left|frac{vec{B} + vec{C}}{2}right|$.
- Tính bình phương độ dài $m_a^2$: $m_a^2 = left|frac{vec{B} + vec{C}}{2}right|^2 = frac{1}{4} |vec{B} + vec{C}|^2$ Nhớ rằng $|vec{X}|^2 = vec{X} cdot vec{X}$ (tích vô hướng). $m_a^2 = frac{1}{4} (vec{B} + vec{C}) cdot (vec{B} + vec{C})$ $m_a^2 = frac{1}{4} (vec{B} cdot vec{B} + 2 vec{B} cdot vec{C} + vec{C} cdot vec{C})$ $m_a^2 = frac{1}{4} (|vec{B}|^2 + 2 vec{B} cdot vec{C} + |vec{C}|^2)$
- Liên hệ với các cạnh của tam giác: Ta có:
- $|vec{B}|^2 = AB^2 = c^2$
- $|vec{C}|^2 = AC^2 = b^2$
- Cạnh BC: $vec{BC} = vec{C} – vec{B}$.
- $BC^2 = |vec{C} – vec{B}|^2 = (vec{C} – vec{B}) cdot (vec{C} – vec{B})$
- $a^2 = |vec{C}|^2 – 2 vec{B} cdot vec{C} + |vec{B}|^2$
- $a^2 = b^2 – 2 vec{B} cdot vec{C} + c^2$
- Từ đây, ta có $2 vec{B} cdot vec{C} = b^2 + c^2 – a^2$.
- Thay thế vào biểu thức $m_a^2$: $m_a^2 = frac{1}{4} (c^2 + (b^2 + c^2 – a^2) + b^2)$ $m_a^2 = frac{1}{4} (2b^2 + 2c^2 – a^2)$
Phương pháp vecto tuy có vẻ trừu tượng hơn một chút nhưng lại rất gọn gàng và hiệu quả, đặc biệt khi làm việc với các bài toán hình học phức tạp hơn hoặc trong không gian nhiều chiều. Nó thể hiện tính đại số của hình học.
Phương Pháp 4: Sử Dụng Hệ Tọa Độ Descartes (Hình Học Giải Tích)
Phương pháp này đặt tam giác vào một hệ tọa độ, sau đó sử dụng các công thức khoảng cách và trung điểm để chứng minh công thức tính đường trung tuyến. Đây là một phương pháp trực quan và rất hữu ích khi làm việc với các tọa độ cụ thể.
Các Bước Chứng Minh:
- Thiết lập hệ tọa độ: Giả sử tam giác ABC được đặt trong hệ tọa độ Oxy. Để đơn giản hóa, ta có thể đặt một đỉnh tại gốc tọa độ và một cạnh nằm trên trục Ox. Đặt B tại gốc tọa độ: $B = (0, 0)$. Đặt C trên trục Ox: $C = (a, 0)$ (độ dài BC là $a$). Đặt A tại tọa độ: $A = (x_A, y_A)$.
- Xác định tọa độ trung điểm M: M là trung điểm của BC. $M = left(frac{0+a}{2}, frac{0+0}{2}right) = left(frac{a}{2}, 0right)$.
- Tính độ dài đường trung tuyến $m_a = AM$: Sử dụng công thức khoảng cách giữa hai điểm $P_1(x_1, y_1)$ và $P_2(x_2, y_2)$ là $sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$. $m_a^2 = AM^2 = left(x_A – frac{a}{2}right)^2 + (y_A – 0)^2$ $m_a^2 = x_A^2 – ax_A + frac{a^2}{4} + y_A^2$ (Phương trình 1)
- Liên hệ với độ dài các cạnh $b$ và $c$:
- Độ dài cạnh $c = AB$: $c^2 = (x_A – 0)^2 + (y_A – 0)^2 = x_A^2 + y_A^2$.
- Độ dài cạnh $b = AC$: $b^2 = (x_A – a)^2 + (y_A – 0)^2 = x_A^2 – 2ax_A + a^2 + y_A^2$.
- Biến đổi để tìm $x_A$ và $y_A$: Từ $c^2 = x_A^2 + y_A^2$, ta có $y_A^2 = c^2 – x_A^2$. Từ $b^2 = x_A^2 – 2ax_A + a^2 + y_A^2$, thay $x_A^2 + y_A^2 = c^2$ vào: $b^2 = c^2 – 2ax_A + a^2$ $2ax_A = a^2 + c^2 – b^2$ $x_A = frac{a^2 + c^2 – b^2}{2a}$
- Thay $x_A$ và $y_A^2$ vào Phương trình 1: $m_a^2 = x_A^2 – ax_A + frac{a^2}{4} + y_A^2$ $m_a^2 = (x_A^2 + y_A^2) – ax_A + frac{a^2}{4}$ $m_a^2 = c^2 – aleft(frac{a^2 + c^2 – b^2}{2a}right) + frac{a^2}{4}$ $m_a^2 = c^2 – frac{a^2 + c^2 – b^2}{2} + frac{a^2}{4}$ $m_a^2 = frac{4c^2 – 2(a^2 + c^2 – b^2) + a^2}{4}$ $m_a^2 = frac{4c^2 – 2a^2 – 2c^2 + 2b^2 + a^2}{4}$ $m_a^2 = frac{2b^2 + 2c^2 – a^2}{4}$
Phương pháp này yêu cầu kỹ năng tính toán đại số nhưng lại cực kỳ hệ thống và ít phụ thuộc vào hình vẽ trực quan, rất phù hợp cho những ai ưa thích sự chính xác của tọa độ. Khác với [công thức tính f vật lý 12] liên quan đến lực và chuyển động, công thức đường trung tuyến lại đi sâu vào cấu trúc và mối quan hệ của các cạnh trong một tam giác, mở ra một thế giới hình học đầy thú vị.
Ứng Dụng Của Công Thức Đường Trung Tuyến Trong Toán Học và Thực Tế
Việc chứng minh công thức tính đường trung tuyến không chỉ là một bài tập lý thuyết mà còn mở ra nhiều cánh cửa ứng dụng thực tiễn trong toán học và các lĩnh vực khác. Nắm vững công thức này cho phép chúng ta giải quyết các vấn đề phức tạp hơn, từ các bài toán hình học thuần túy đến những ứng dụng trong khoa học kỹ thuật.
Giải Quyết Các Bài Toán Hình Học Phức Tạp
Công thức đường trung tuyến là một công cụ mạnh mẽ để:
- Tính độ dài đường trung tuyến: Khi biết độ dài ba cạnh của tam giác, ta có thể dễ dàng tính được độ dài của ba đường trung tuyến. Điều này đặc biệt hữu ích trong các bài toán yêu cầu xác định các yếu tố của tam giác.
- Xác định loại tam giác: Đôi khi, các bài toán đưa ra thông tin về độ dài các đường trung tuyến và yêu cầu xác định loại tam giác (ví dụ: tam giác cân, tam giác vuông). Bằng cách sử dụng ngược công thức, ta có thể tìm ra mối quan hệ giữa các cạnh. Ví dụ, trong một tam giác vuông tại A, đường trung tuyến ứng với cạnh huyền là nửa cạnh huyền ($m_a = frac{a}{2}$). Thay vào công thức, ta có thể thấy mối liên hệ này.
- Chứng minh các định lý khác: Công thức đường trung tuyến có thể là một bước trung gian hoặc một phần của việc chứng minh các định lý hình học phức tạp hơn, chẳng hạn như định lý về mối quan hệ giữa các đường trung tuyến và diện tích tam giác.
- Bài toán về diện tích: Mặc dù không trực tiếp tính diện tích, nhưng độ dài đường trung tuyến có thể được sử dụng kết hợp với các công thức khác (ví dụ: công thức Heron) để tìm diện tích khi các thông số khác được biết đến.
Liên Hệ Với Định Lý Apollonius
Như đã đề cập, công thức tính đường trung tuyến chính là một phát biểu khác của Định lý Apollonius. Định lý này không chỉ áp dụng cho tam giác mà còn có thể mở rộng cho các bài toán liên quan đến tứ giác, khi chia tứ giác thành các tam giác nhỏ. Trong khoa học, việc xác định [hệ số tương quan định luật beer] giúp ta hiểu rõ mối liên hệ giữa các đại lượng, cũng cũng như cách các công thức toán học mô tả các mối quan hệ hình học.
Vai Trò Trong Các Lĩnh Vực Kỹ Thuật, Kiến Trúc và Vật Lý
Mặc dù công thức đường trung tuyến chủ yếu là một công cụ toán học, nhưng các nguyên lý hình học mà nó đại diện lại có ứng dụng rộng rãi:
- Thiết kế và Kiến trúc: Trong thiết kế kiến trúc, các kỹ sư thường phải tính toán các yếu tố cân bằng, phân bố lực trên các cấu trúc hình tam giác. Việc xác định trọng tâm (giao điểm của các đường trung tuyến) là rất quan trọng để đảm bảo sự ổn định của công trình. Chẳng hạn, khi thiết kế cầu, mái nhà, hoặc các khung giàn, việc biết vị trí trọng tâm giúp tối ưu hóa vật liệu và đảm bảo an toàn.
- Vật lý (Cơ học): Trọng tâm của một vật thể phẳng hình tam giác đồng chất chính là giao điểm của ba đường trung tuyến. Đây là điểm mà tại đó toàn bộ khối lượng của vật thể có thể coi là tập trung. Việc tìm trọng tâm là bước cơ bản trong việc phân tích lực, mômen lực và chuyển động của vật thể. Điều này có ứng dụng trong việc thiết kế các bộ phận máy móc, cân bằng các vật thể quay, hoặc phân tích sự ổn định của phương tiện.
- Hệ thống định vị và robot: Trong một số hệ thống định vị hoặc robot, việc tính toán các điểm trung tâm hoặc các vị trí cân bằng của các cấu trúc dạng tam giác có thể sử dụng các nguyên lý tương tự như công thức đường trung tuyến.
Việc chứng minh công thức tính đường trung tuyến và hiểu các ứng dụng của nó không chỉ làm sâu sắc thêm kiến thức toán học mà còn giúp chúng ta nhận ra mối liên hệ giữa lý thuyết và thực tiễn, từ đó nâng cao khả năng giải quyết vấn đề trong nhiều ngữ cảnh khác nhau.
Những Sai Lầm Thường Gặp Khi Áp Dụng và Chứng Minh Công Thức
Mặc dù công thức tính đường trung tuyến tương đối đơn giản, nhưng trong quá trình áp dụng và chứng minh công thức tính đường trung tuyến, người học vẫn có thể mắc phải một số sai lầm phổ biến. Việc nhận diện và tránh những sai lầm này là rất quan trọng để đảm bảo tính chính xác và hiệu quả trong học tập cũng như giải quyết bài tập.
Nhầm Lẫn Các Biến Trong Công Thức
Đây là sai lầm cơ bản nhưng rất thường gặp. Công thức cho $m_a$ là $m_a^2 = frac{2b^2 + 2c^2 – a^2}{4}$. Nhiều học sinh có thể nhầm lẫn vị trí của các cạnh, ví dụ như viết $m_a^2 = frac{2a^2 + 2b^2 – c^2}{4}$ hoặc các biến thể khác.
- Giải pháp: Luôn nhớ rằng cạnh $a$ là cạnh đối diện với đỉnh A, và $m_a$ là đường trung tuyến xuất phát từ đỉnh A. Trong công thức của $m_a$, cạnh $a^2$ sẽ mang dấu âm, và hai cạnh còn lại ($b^2, c^2$) sẽ mang dấu dương và được nhân đôi. Luôn kiểm tra lại các ký hiệu cẩn thận.
Sai Sót Trong Quá Trình Tính Toán Đại Số
Các phương pháp chứng minh công thức đường trung tuyến, đặc biệt là phương pháp dùng định lý Cosin hay hệ tọa độ Descartes, thường liên quan đến các phép biến đổi đại số. Các sai sót nhỏ như quên dấu, chia sai, hoặc cộng trừ nhầm lẫn có thể dẫn đến kết quả sai hoàn toàn.
- Ví dụ: Khi cộng hai phương trình trong phương pháp Định lý Cosin, nếu không để ý dấu của $am_a cos alpha$ và $-am_a cos alpha$, có thể dẫn đến việc không triệt tiêu được số hạng này.
- Giải pháp: Thực hiện từng bước biến đổi một cách cẩn thận, viết rõ ràng các phương trình trung gian. Sử dụng nháp để kiểm tra lại các phép tính phức tạp.
Quên Điều Kiện Áp Dụng Hoặc Các Giả Định Cơ Bản
Mỗi định lý và công thức đều có những điều kiện áp dụng nhất định. Mặc dù công thức đường trung tuyến áp dụng cho mọi loại tam giác, nhưng trong quá trình chứng minh hoặc khi kết hợp với các định lý khác, việc quên các giả định (ví dụ: M là trung điểm) có thể gây nhầm lẫn.
- Giải pháp: Đảm bảo rằng bạn đã hiểu rõ các điều kiện của các định lý phụ trợ (như Định lý Cosin, Định lý Stewart) trước khi áp dụng chúng. Ví dụ, trong phương pháp Định lý Stewart, việc xác định đúng các đoạn $m, n$ là rất quan trọng.
Không Hiểu Rõ Bản Chất Hình Học
Đôi khi, học sinh chỉ học thuộc lòng công thức và các bước chứng minh mà không thực sự hiểu ý nghĩa hình học đằng sau. Điều này khiến họ khó khăn khi gặp các bài toán biến thể hoặc cần suy luận sâu hơn.
- Ví dụ: Trong phương pháp Định lý Cosin, việc hiểu rằng $cos(180^circ – alpha) = -cos alpha$ là rất quan trọng. Nếu không hiểu rõ mối quan hệ giữa các góc kề bù, quá trình chứng minh sẽ bị gián đoạn.
- Giải pháp: Luôn cố gắng hình dung hình vẽ, hiểu mối quan hệ giữa các cạnh, góc và đường thẳng. Tự mình vẽ lại hình và thử lại các bước chứng minh để củng cố sự hiểu biết. Việc giải các [bài tập tự luận định luật 2 newton] cũng đòi hỏi sự hiểu biết sâu sắc về nguyên lý vật lý, tương tự như việc áp dụng công thức đường trung tuyến cũng yêu cầu sự nắm vững các định lý hình học.
Thiếu Luyện Tập và Vận Dụng
Giống như bất kỳ kiến thức toán học nào khác, việc thành thạo công thức đường trung tuyến đòi hỏi sự luyện tập thường xuyên. Nếu chỉ đọc qua mà không thực hành, kiến thức sẽ dễ bị mai một.
- Giải pháp: Làm nhiều bài tập vận dụng từ cơ bản đến nâng cao. Tự mình thử lại các phương pháp chứng minh mà không nhìn tài liệu để kiểm tra mức độ nắm vững.
Việc nhận thức và chủ động khắc phục những sai lầm này sẽ giúp quá trình học tập và ứng dụng công thức tính đường trung tuyến trở nên hiệu quả và chính xác hơn rất nhiều.
Bài Tập Vận Dụng Công Thức Đường Trung Tuyến
Sau khi đã tìm hiểu và chứng minh công thức tính đường trung tuyến qua nhiều phương pháp, việc thực hành giải bài tập là bước không thể thiếu để củng cố kiến thức. Các bài tập sau đây sẽ giúp bạn áp dụng công thức vào các trường hợp cụ thể, từ đó nắm vững cách sử dụng và ý nghĩa của nó.
Bài Tập 1: Tính Độ Dài Đường Trung Tuyến Trong Tam Giác Thường
Đề bài: Cho tam giác ABC có độ dài các cạnh $AB = c = 7$ cm, $AC = b = 5$ cm và $BC = a = 8$ cm. Tính độ dài đường trung tuyến $m_a$ (từ đỉnh A đến cạnh BC).
Lời giải: Áp dụng công thức tính đường trung tuyến $m_a^2 = frac{2b^2 + 2c^2 – a^2}{4}$. Thay các giá trị đã cho vào công thức: $m_a^2 = frac{2(5^2) + 2(7^2) – 8^2}{4}$ $m_a^2 = frac{2(25) + 2(49) – 64}{4}$ $m_a^2 = frac{50 + 98 – 64}{4}$ $m_a^2 = frac{148 – 64}{4}$ $m_a^2 = frac{84}{4}$ $m_a^2 = 21$ Vậy, $m_a = sqrt{21}$ cm.
Bài Tập 2: Xác Định Loại Tam Giác Khi Biết Độ Dài Các Đường Trung Tuyến
Đề bài: Một tam giác có độ dài các cạnh là $a, b, c$. Biết rằng $m_a = m_b$. Chứng minh tam giác đó là tam giác cân.
Lời giải: Ta có công thức tính đường trung tuyến: $m_a^2 = frac{2b^2 + 2c^2 – a^2}{4}$ $m_b^2 = frac{2a^2 + 2c^2 – b^2}{4}$ Theo đề bài, $m_a = m_b$, suy ra $m_a^2 = m_b^2$. $frac{2b^2 + 2c^2 – a^2}{4} = frac{2a^2 + 2c^2 – b^2}{4}$ Nhân cả hai vế với 4: $2b^2 + 2c^2 – a^2 = 2a^2 + 2c^2 – b^2$ Trừ $2c^2$ ở cả hai vế: $2b^2 – a^2 = 2a^2 – b^2$ Chuyển các số hạng có $a^2$ và $b^2$ về cùng một vế: $2b^2 + b^2 = 2a^2 + a^2$ $3b^2 = 3a^2$ $b^2 = a^2$ Vì độ dài các cạnh luôn dương, nên $b = a$. Vậy, tam giác ABC có hai cạnh $a$ và $b$ bằng nhau, nên tam giác đó là tam giác cân tại C.
Bài Tập 3: Ứng Dụng Trong Tam Giác Vuông
Đề bài: Cho tam giác ABC vuông tại A. Gọi M là trung điểm của cạnh huyền BC. Biết $AB = 6$ cm, $AC = 8$ cm. Tính độ dài đường trung tuyến AM.
Lời giải: Trong tam giác vuông ABC tại A, theo Định lý Pytago, ta có: $BC^2 = AB^2 + AC^2 = 6^2 + 8^2 = 36 + 64 = 100$. Vậy, $BC = a = 10$ cm. Độ dài các cạnh của tam giác là $a = 10$ cm, $b = AC = 8$ cm, $c = AB = 6$ cm. Áp dụng công thức tính đường trung tuyến $m_a$ (đường trung tuyến ứng với cạnh huyền BC): $m_a^2 = frac{2b^2 + 2c^2 – a^2}{4}$ $m_a^2 = frac{2(8^2) + 2(6^2) – 10^2}{4}$ $m_a^2 = frac{2(64) + 2(36) – 100}{4}$ $m_a^2 = frac{128 + 72 – 100}{4}$ $m_a^2 = frac{200 – 100}{4}$ $m_a^2 = frac{100}{4}$ $m_a^2 = 25$ Vậy, $m_a = sqrt{25} = 5$ cm. Nhận xét: Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền. $m_a = AM = frac{1}{2}BC = frac{1}{2}(10) = 5$ cm. Kết quả này khớp với công thức đã chứng minh, cho thấy sự nhất quán của các định lý hình học. Tương tự như [công thức tính f vật lý 12] giúp ta giải quyết các bài toán về lực, công thức đường trung tuyến là nền tảng để giải quyết nhiều vấn đề hình học.
Những bài tập này không chỉ giúp bạn làm quen với việc sử dụng công thức mà còn rèn luyện khả năng phân tích và giải quyết vấn đề trong hình học.
Kết Luận
Qua bài viết này, chúng ta đã cùng nhau khám phá sâu rộng về đường trung tuyến trong tam giác, từ định nghĩa, các tính chất cơ bản đến các phương pháp chi tiết để chứng minh công thức tính đường trung tuyến. Dù là sử dụng Định lý Cosin, Định lý Stewart, phương pháp Vecto hay Hình học giải tích, mỗi cách tiếp cận đều mang lại một cái nhìn sâu sắc và củng cố hiểu biết về vẻ đẹp logic của toán học. Việc nắm vững công thức tính đường trung tuyến không chỉ là một cột mốc quan trọng trong học tập hình học mà còn là nền tảng vững chắc để giải quyết nhiều bài toán phức tạp hơn, từ đó ứng dụng vào các lĩnh vực như kỹ thuật, kiến trúc. Hy vọng rằng những kiến thức được trình bày đã cung cấp một cái nhìn toàn diện và giúp bạn tự tin hơn trong hành trình chinh phục môn Toán.
