Hướng dẫn cách tìm tham số m lớp 9

n

1. Kiến thức cần nhớ để giải bài toán tìm tham số m lớp 9

n

n

Nếu hai số có tổng bằng S và tích bằng P thì hai số đó là hai nghiệm của phương trình: x2- Sx + P = 0 (1).

n

Chú ý: điều kiện S2 – 4P ≥ 0 là bắt buộc. Đây là điều kiện để ∆ (1) ≥ 0 hay nói cách khác, đây là điều kiện để phương trình bậc 2 tồn tại nghiệm.

n

👉 Ôn tập định lý Vi-ét thuận, định lý Vi-ét đảo

👉 Gợi ý các phần mềm học tập và ôn thi hiệu quả cho học sinh lớp 9

n

[%Included.Lớp 9%]

n

2. Hướng dẫn cách tìm tham số m lớp 9

n

2.1. Dạng 1: Tìm m để phương trình có nghiệm thỏa mãn điều kiện: âm, dương, cùng dấu, trái dấu

n

n

Bài toán 1: Tìm điều kiện của tham số để phương trình sau có hai nghiệm phân biệt cùng dấu: 3×2 – 4mx + m2 – 2m – 3 = 0

n

Hướng dẫn giải

n

n

n

[%Included.Dangky%]

n

Bài toán 2: Tìm điều kiện của tham số để phương trình sau có hai nghiệm phân biệt cùng dấu dương: 3×2 – 4mx + m2 – 2m – 3 = 0

n

Hướng dẫn giải

n

n

👉 Bài tập tìm m để phương trình có nghiệm thỏa mãn điều kiện: âm, dương, cùng dấu, trái dấu

n

2.2. Dạng 2: Tìm m để phương trình có nghiệm thỏa mãn điều kiện đối xứng giữa x1, x2

n

Phương pháp giải: Cho phương trình ax2 + bx + c = 0 (a ≠ 0)

• n
• Bước 1: Tìm điều kiện để phương trình có nghiệm.n
• Bước 2: Sử dụng hệ thức Vi-ét, kết hợp biến đổi theo điều kiện đối xứng giữa x1, x2.n
• Bước 3: Kết luận.n

n

Bài toán 1:Cho phương trình x2 – 4mx + 4 = 0. Tìm m để phương trình có hai nghiệm phân biệt thỏa mãn x12 + x22 = 56

n

Hướng dẫn giải

n

n

n

Bài toán 2: Cho phương trình x2 – x + 1 + m = 0. Tìm m để phương trình có hai nghiệm phân biệt thỏa mãn (x1 + 1)2 + (x2 + 1)2 = 3

n

Hướng dẫn giải

n

n

n

👉 Bài tập tìm m để phương trình có nghiệm thỏa mãn điều kiện đối xứng giữa x1, x2

n

2.3. Dạng 3: Tìm m để phương trình có nghiệm thỏa mãn điều kiện không đối xứng

n

n

Bài toán: Cho phương trình x2 – mx – m – 1 = 0. Tìm m để phương trình có hai nghiệm phân biệt x1, x2 thỏa mãn 2×1 – 3×2 = 5 theo hai cách.

n

Hướng dẫn giải

n

n

n

n

👉 Bài tập tìm m để phương trình có nghiệm thỏa mãn điều kiện không đối xứng

n

2.4. Dạng 4: Tìm m để phương trình có nghiệm thỏa mãn điều kiện số học

n

Phương pháp giải: Cho phương trình ax2 + bx + c = 0 (a ≠ 0)

• n
• Bước 1: Tìm điều kiện để phương trình có nghiệm.n
• Bước 2: Sử dụng hệ thức Vi-ét, kết hợp biến đổi theo điều kiện số học đã cho.n
• Bước 3: Kết luận.n

n

Bài toán 1: Cho phương trình x2 – (m + 2)x – 3 = 0. Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt là các số nguyên.

n

Hướng dẫn giải

n

n

n

Bài toán 2: Cho phương trình x2 – 20x + m + 5 = 0. Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt là các số nguyên tố.

n

Hướng dẫn giải

n

n

n

👉 Bài tập tìm m để phương trình có nghiệm thỏa mãn điều kiện số học

n

2.5. Dạng 5: Tìm m để phương trình có nghiệm thỏa mãn điều kiện về cực trị

n

Phương pháp giải: Cho phương trình ax2 + bx + c = 0 (a ≠ 0)

• n
• Bước 1: Tìm điều kiện để phương trình có hai nghiệm phân biệt.n
• Bước 2: Sử dụng hệ thức Vi-ét, kết hợp biến đổi biểu thức.n
• Bước 3: Đánh giá biểu thức tìm được.n
• Bước 4: Kết luận.n

n

Bài toán:Cho phương trình x2 + 2(m -1)x – 2m = 0. Tìm m để phương trình có hai nghiệm sao cho A = (x1 – x2)2 đạt giá trị nhỏ nhất.

n

Hướng dẫn giải

n

n

n

👉 Bài tập tìm m để phương trình có nghiệm thỏa mãn điều kiện về cực trị

n

Như vậy, bài viết trên đã giới thiệu các kiến thức cần nhớ để giải bài toán tìm tham số m lớp 9 và hướng dẫn cách tìm tham số m lớp 9 chi tiết qua từng dạng bài toán. Hy vọng các bạn sẽ ghi nhớ và áp dụng hiệu quả vào các bài tập cụ thể trong quá trình ôn thi vào 10.

n

[%Included.TAK12%]

“,”startDateUtc”:”2024-07-31T17:00:00″,”startDate”:”2024-08-01T00:00:00+07:00″,”allowComments”:false,”createdOnUtc”:”2024-07-09T05:01:03.513745″,”createdOn”:”2024-07-09T12:01:03.513745+07:00″,”author”:null,”readCount”:0,”newsTags”:[{“name”:”Toán lớp 9″,”seName”:”toan-lop-9″,”id”:1853}],”publishedDate”:”2024-08-01T00:00:00+07:00″,”metaKeywords”:null,”metaDescription”:”Cách tìm tham số m là gì? Kiến thức cần nhớ để tìm điều kiện tham số m. Hướng dẫn cách tìm tham số m lớp 9 qua những dạng bài thường gặp với bài tập minh họa có lời giải chi tiết. Xem ngay!”,”metaTitle”:”Hướng dẫn cách tìm tham số m lớp 9″,”isShowSignInForm”:true,”id”:1889};

Tìm tham số m để phương trình có nghiệm thỏa mãn điều kiện là một trong những dạng bài thường gặp khi ôn luyện toán vào lớp 10. Bài viết sau đây TAK12 sẽ chia sẻ cách tìm tham số m lớp 9 theo từng dạng bài cùng bài tập minh họa. Các em học sinh hãy đón đọc nhé!

1. Kiến thức cần nhớ để giải bài toán tìm tham số m lớp 9

Nếu hai số có tổng bằng S và tích bằng P thì hai số đó là hai nghiệm của phương trình: x2- Sx + P = 0 (1).

Chú ý: điều kiện S2 – 4P ≥ 0 là bắt buộc. Đây là điều kiện để ∆ (1) ≥ 0 hay nói cách khác, đây là điều kiện để phương trình bậc 2 tồn tại nghiệm.

👉 Ôn tập định lý Vi-ét thuận, định lý Vi-ét đảo

👉 Gợi ý các phần mềm học tập và ôn thi hiệu quả cho học sinh lớp 9

[%Included.Lớp 9%]

2. Hướng dẫn cách tìm tham số m lớp 9

2.1. Dạng 1: Tìm m để phương trình có nghiệm thỏa mãn điều kiện: âm, dương, cùng dấu, trái dấu

Bài toán 1: Tìm điều kiện của tham số để phương trình sau có hai nghiệm phân biệt cùng dấu: 3×2 – 4mx + m2 – 2m – 3 = 0

Hướng dẫn giải

[%Included.Dangky%]

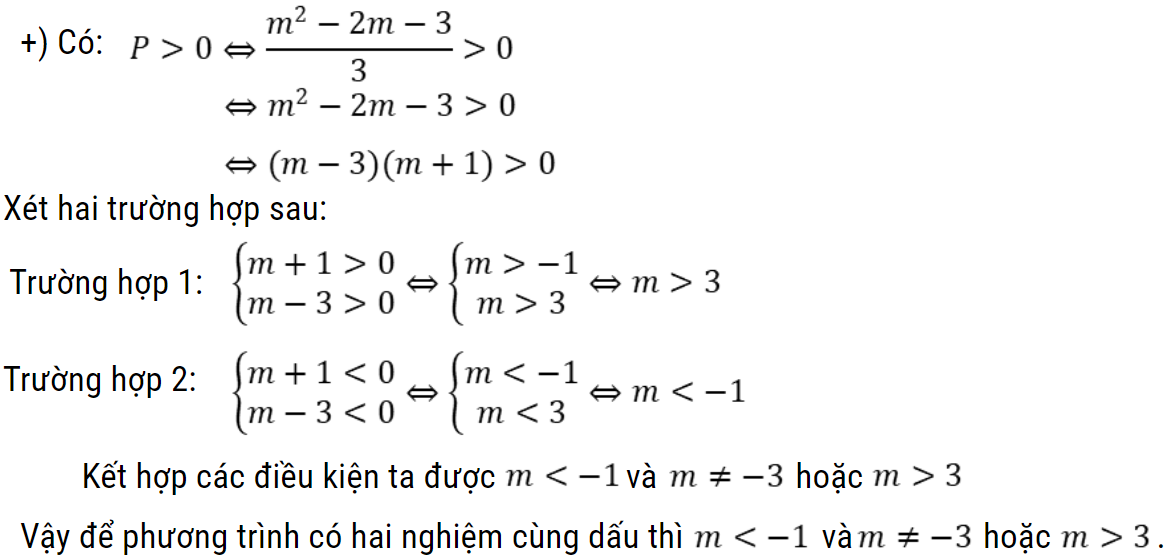
Bài toán 2: Tìm điều kiện của tham số để phương trình sau có hai nghiệm phân biệt cùng dấu dương: 3×2 – 4mx + m2 – 2m – 3 = 0

Hướng dẫn giải

👉 Bài tập tìm m để phương trình có nghiệm thỏa mãn điều kiện: âm, dương, cùng dấu, trái dấu

2.2. Dạng 2: Tìm m để phương trình có nghiệm thỏa mãn điều kiện đối xứng giữa x1, x2

Phương pháp giải: Cho phương trình ax2 + bx + c = 0 (a ≠ 0)

• Bước 1: Tìm điều kiện để phương trình có nghiệm.
• Bước 2: Sử dụng hệ thức Vi-ét, kết hợp biến đổi theo điều kiện đối xứng giữa x1, x2.
• Bước 3: Kết luận.

Bài toán 1:Cho phương trình x2 – 4mx + 4 = 0. Tìm m để phương trình có hai nghiệm phân biệt thỏa mãn x12 + x22 = 56

Hướng dẫn giải

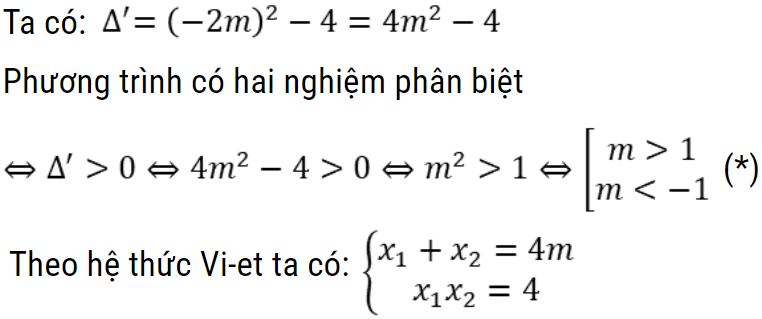
Bài toán 2: Cho phương trình x2 – x + 1 + m = 0. Tìm m để phương trình có hai nghiệm phân biệt thỏa mãn (x1 + 1)2 + (x2 + 1)2 = 3

Hướng dẫn giải

👉 Bài tập tìm m để phương trình có nghiệm thỏa mãn điều kiện đối xứng giữa x1, x2

2.3. Dạng 3: Tìm m để phương trình có nghiệm thỏa mãn điều kiện không đối xứng

Bài toán: Cho phương trình x2 – mx – m – 1 = 0. Tìm m để phương trình có hai nghiệm phân biệt x1, x2 thỏa mãn 2×1 – 3×2 = 5 theo hai cách.

Hướng dẫn giải

👉 Bài tập tìm m để phương trình có nghiệm thỏa mãn điều kiện không đối xứng

2.4. Dạng 4: Tìm m để phương trình có nghiệm thỏa mãn điều kiện số học

Phương pháp giải: Cho phương trình ax2 + bx + c = 0 (a ≠ 0)

• Bước 1: Tìm điều kiện để phương trình có nghiệm.
• Bước 2: Sử dụng hệ thức Vi-ét, kết hợp biến đổi theo điều kiện số học đã cho.
• Bước 3: Kết luận.

Bài toán 1: Cho phương trình x2 – (m + 2)x – 3 = 0. Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt là các số nguyên.

Hướng dẫn giải

Bài toán 2: Cho phương trình x2 – 20x + m + 5 = 0. Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt là các số nguyên tố.

Hướng dẫn giải

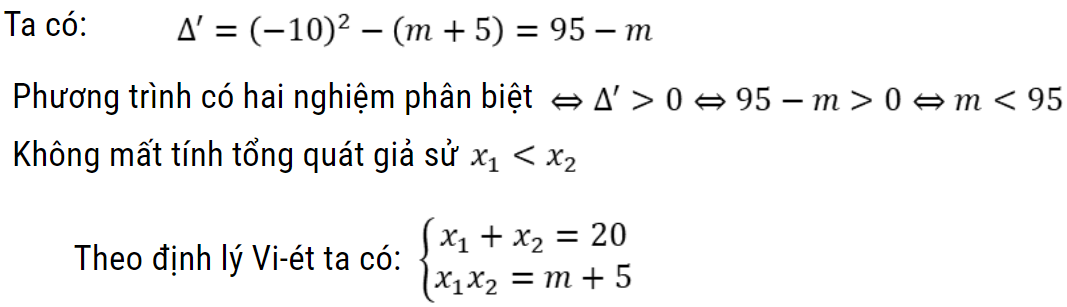
👉 Bài tập tìm m để phương trình có nghiệm thỏa mãn điều kiện số học

2.5. Dạng 5: Tìm m để phương trình có nghiệm thỏa mãn điều kiện về cực trị

Phương pháp giải: Cho phương trình ax2 + bx + c = 0 (a ≠ 0)

• Bước 1: Tìm điều kiện để phương trình có hai nghiệm phân biệt.
• Bước 2: Sử dụng hệ thức Vi-ét, kết hợp biến đổi biểu thức.
• Bước 3: Đánh giá biểu thức tìm được.
• Bước 4: Kết luận.

Bài toán:Cho phương trình x2 + 2(m -1)x – 2m = 0. Tìm m để phương trình có hai nghiệm sao cho A = (x1 – x2)2 đạt giá trị nhỏ nhất.

Hướng dẫn giải

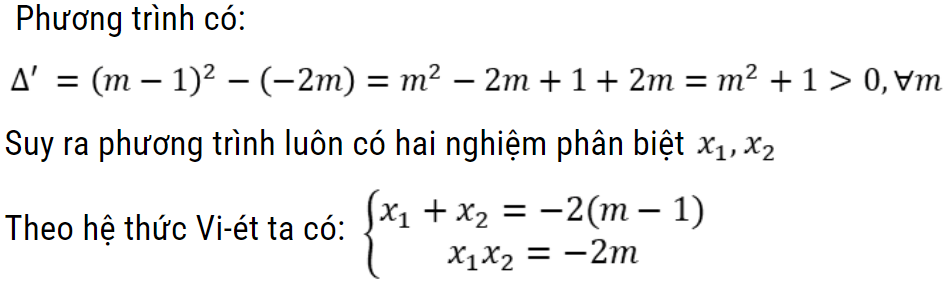
👉 Bài tập tìm m để phương trình có nghiệm thỏa mãn điều kiện về cực trị

Như vậy, bài viết trên đã giới thiệu các kiến thức cần nhớ để giải bài toán tìm tham số m lớp 9 và hướng dẫn cách tìm tham số m lớp 9 chi tiết qua từng dạng bài toán. Hy vọng các bạn sẽ ghi nhớ và áp dụng hiệu quả vào các bài tập cụ thể trong quá trình ôn thi vào 10.

[%Included.TAK12%]