a) Tập xác định: (D = mathbb{R}).
Ta có: (y’ = 3{x^2} – 6x + 3 = 3{left( {x – 1} right)^2},y’ = 0 Leftrightarrow x = 1)
Lập bảng biến thiên của hàm số:
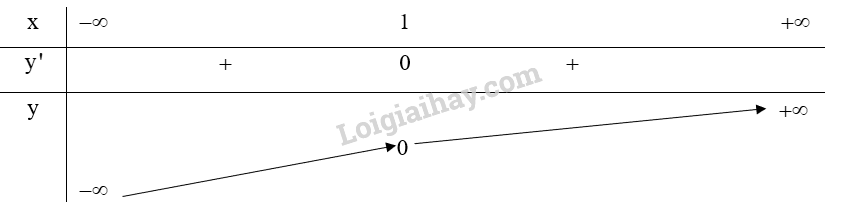
Hàm số (y = {x^3} – 3{x^2} + 3x – 1) đồng biến trên khoảng (left( { – infty ;1} right)) và (left( {1; + infty } right)).
Hàm số (y = {x^3} – 3{x^2} + 3x – 1) không có cực trị.
b) Tập xác định của hàm số là (D = mathbb{R}).
Ta có: (y’ = 4{x^3} – 4x,y’ = 0 Leftrightarrow 4{x^3} – 4x = 0 Leftrightarrow left[ begin{array}{l}x = 0x = pm 1end{array} right.)
Bảng biến thiên:
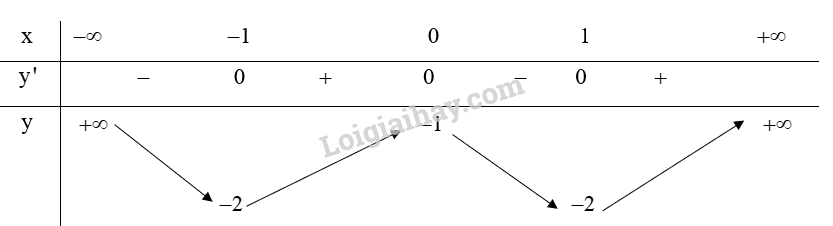
Từ bảng biến thiên ta có:
Hàm số (y = {x^4} – 2{x^2} – 1) đồng biến trên khoảng (left( { – 1;0} right)) và (left( {1; + infty } right)).
Hàm số (y = {x^4} – 2{x^2} – 1) nghịch biến trên khoảng (left( { – infty ; – 1} right)) và (left( {0;1} right)).
Hàm số (y = {x^4} – 2{x^2} – 1) đạt cực đại tại (x = 0) và .
Hàm số (y = {x^4} – 2{x^2} – 1) đạt cực tiểu tại (x = pm 1) và ({y_{CT}} = – 2).
c) Tập xác định: (D = mathbb{R}backslash left{ { – frac{1}{3}} right}).
Ta có: (y’ = frac{{2left( {3x + 1} right) – 3left( {2x – 1} right)}}{{{{left( {3x + 1} right)}^2}}} = frac{5}{{{{left( {3x + 1} right)}^2}}} > 0;forall x ne frac{{ – 1}}{3})
Lập bảng biến thiên của hàm số:
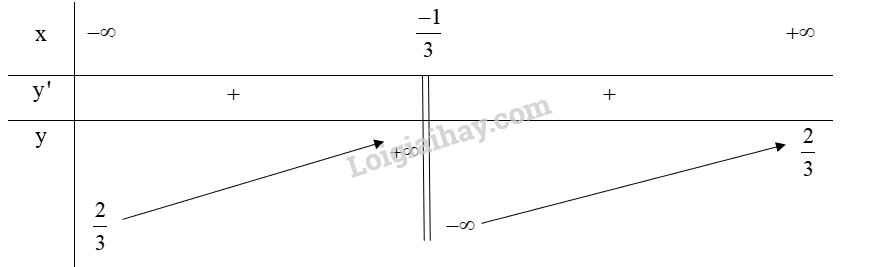
Từ bảng biến thiên ta có:
Hàm số (y = frac{{2x – 1}}{{3x + 1}}) đồng biến trên (left( { – infty ;frac{{ – 1}}{3}} right)) và (left( {frac{{ – 1}}{3}; + infty } right)).
Hàm số không có cực trị.
d) Tập xác định: (D = mathbb{R}backslash left{ { – 1} right}).
Ta có: (y’ = frac{{left( {2x + 2} right)left( {x + 1} right) – left( {{x^2} + 2x + 2} right)}}{{{{left( {x + 1} right)}^2}}} = frac{{{x^2} + 2x}}{{{{left( {x + 1} right)}^2}}})
(y’ = 0 Leftrightarrow left[ begin{array}{l}x = 0x = – 2end{array} right.) (thỏa mãn)
Lập bảng biến thiên của hàm số:
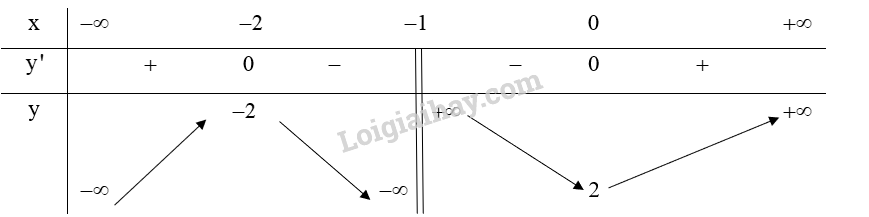
Từ bảng biến thiên ta có:
Hàm số (y = frac{{{x^2} + 2x + 2}}{{x + 1}}) đồng biến trên khoảng (left( { – infty ; – 2} right)) và (left( {0; + infty } right)).
Hàm số (y = frac{{{x^2} + 2x + 2}}{{x + 1}}) nghịch biến trên khoảng (left( { – 2; – 1} right)) và (left( { – 1;0} right)).
Hàm số (y = frac{{{x^2} + 2x + 2}}{{x + 1}}) đạt cực đại tại (x = – 2) và .
Hàm số (y = frac{{{x^2} + 2x + 2}}{{x + 1}}) đạt cực tiểu tại (x = 0) và ({y_{CT}} = 2).
