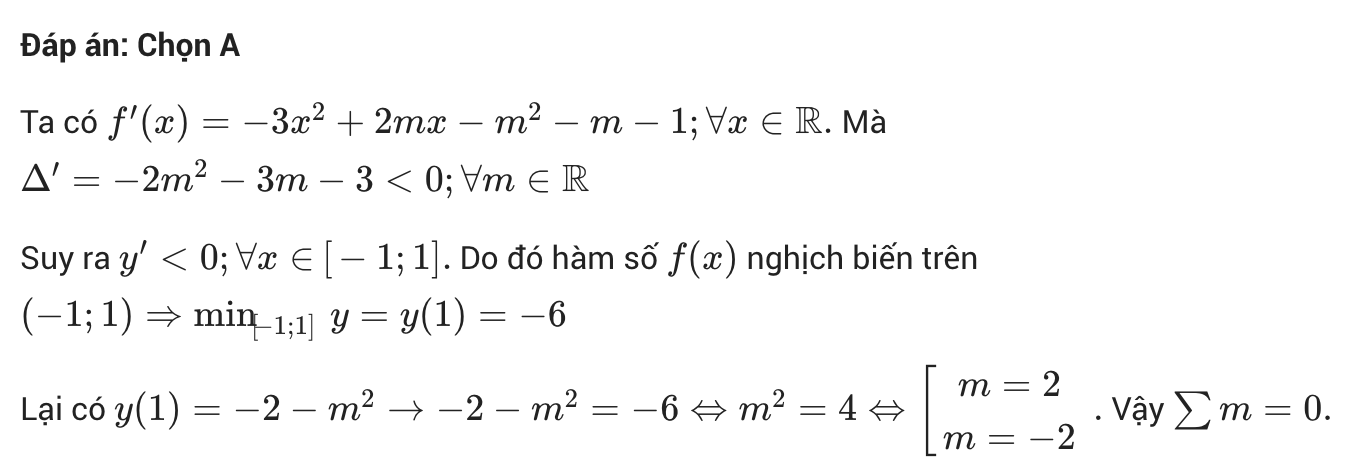Tìm m để hàm số đạt giá trị lớn nhất và tìm m để giá trị nhỏ nhất của hàm số là 2 dạng bài tập phổ biến thường hay xuất hiện trong đề kiểm tra, đề thi học kì môn toán 12. Cùng butbi ôn luyện kiến thức nhé!
Tham khảo thêm:
- Tìm giá trị lớn nhất nhỏ nhất của hàm số
- Giải Toán 12
Tìm m để hàm số đạt giá trị lớn nhất (ví dụ minh họa)
Bài tập 1:
Đề bài: Tìm giá trị thực của tham số m để cho hàm số f(x)= -x² + 4x − m đạt giá trị lớn nhất ở trên đoạn [-1;3] bằng 10.
Lựa chọn đáp án:
- A. m= 1
- B. m= -6
- C. m= -5
- D. m= -2
Lời giải:
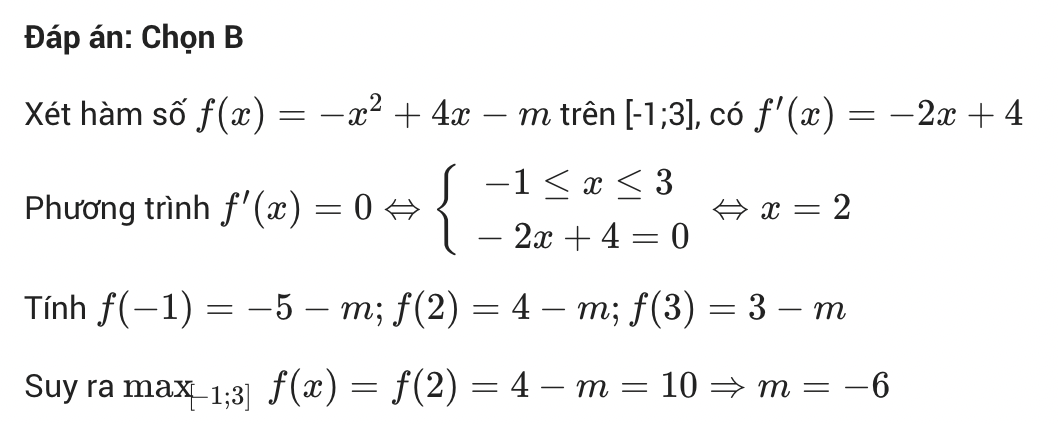
Bài tập 2:
Đề bài: Cho hàm số với m là tham số thực. Tìm giá trị lớn nhất của m để hàm số đã cho có giá trị nhỏ nhất trên đoạn [0;3] bằng – 2.
Lựa chọn đáp án:
- A. m= -4
- B. m= 2
- C. m= 4
- D. m= -2
Lời giải:
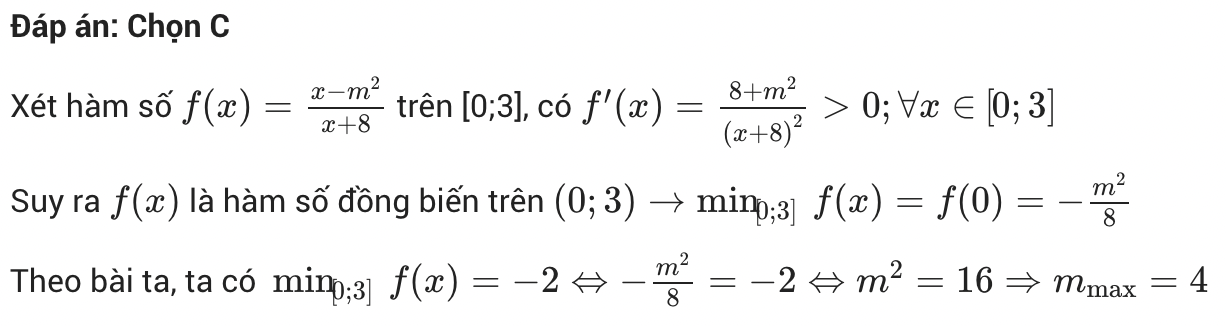
Bài tập 3:
Đề bài: Có tổng bao nhiêu giá trị của m để giá trị lớn nhất của hàm số nằm trên đoạn [0;4] bằng -1.
Lựa chọn đáp án:
- A. 5
- B. 4
- C. 1
- D. 6
Lời giải:

Bài tập 4:
Đề bài: Có bao nhiêu số thực m để cho hàm số có giá trị lớn nhất trên khoảng [-3;2] bằng 150?
Lựa chọn đáp án:
- A. 2
- B. 1
- C. 3
- D. 5
Lời giải:
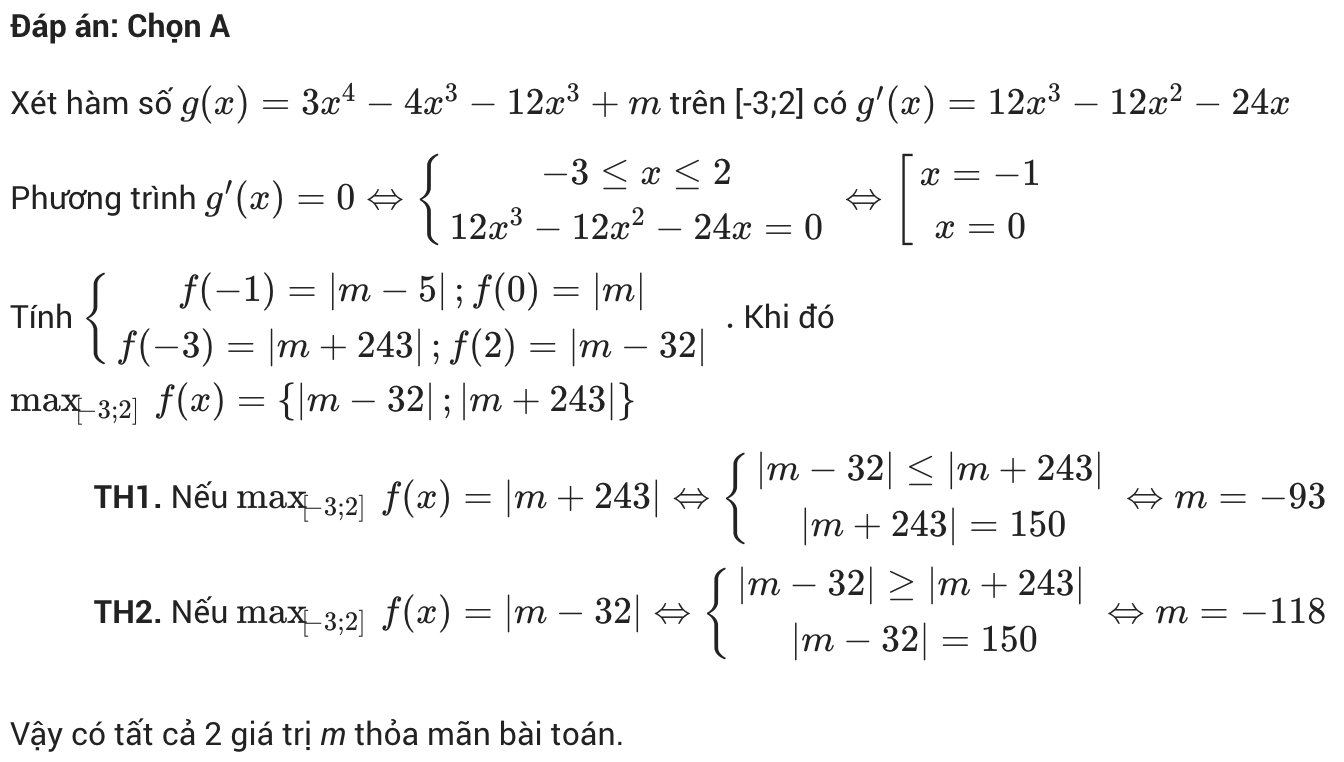
Bài tập 5:
Đề bài: Tìm các giá trị của m sao cho giá trị lớn nhất của hàm số y = x2 – 2x + m trong đoạn [-1; 2] bằng 5.
Lời giải:

Tìm m để hàm số đạt giá trị nhỏ nhất (ví dụ minh họa)
Bài tập 1:
Đề bài: Cho hàm số sau f(x) = x3 + (m2 + 1)x + m2 – 2 với m là số thực. Hãy tìm tất cả các giá trị của m sao cho hàm số có giá trị nhỏ nhất ở trên đoạn [0; 2] bằng 7.
Lời giải:
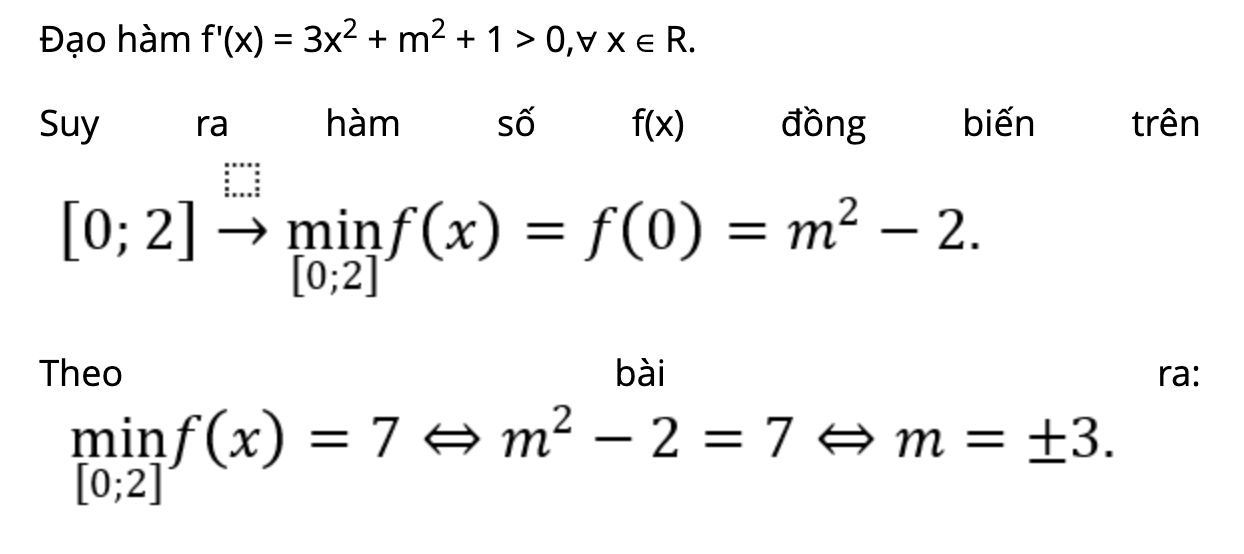
Bài tập 2:
Đề bài: Cho hàm số với tham số thực là m. Hãy tìm tất cả các giá trị của m sao cho hàm số có giá trị nhỏ nhất trên đoạn [0; 1] có kết quả bằng -2.
Lời giải:
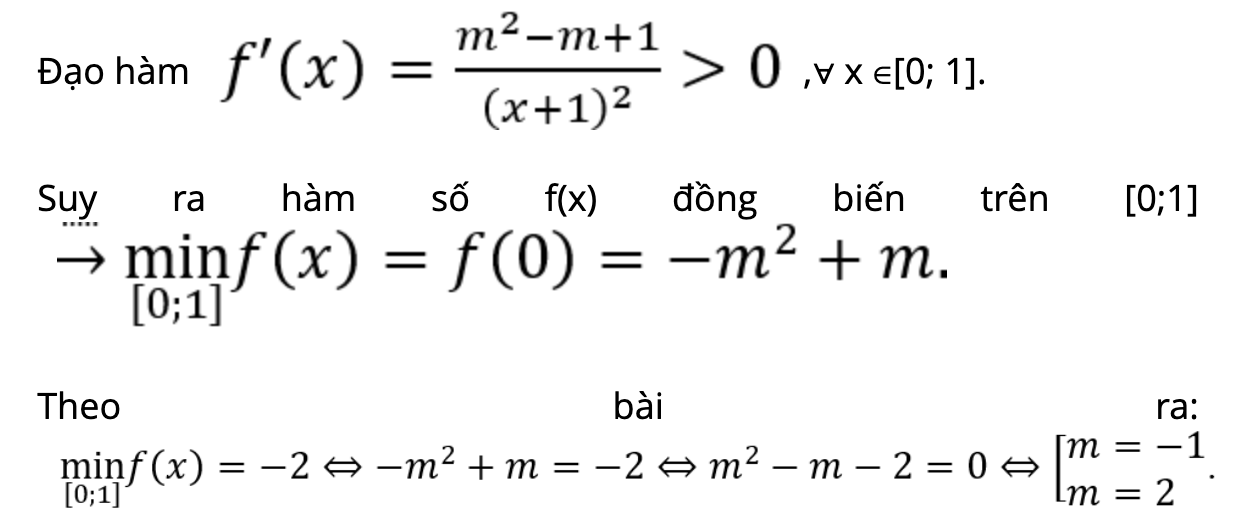
Bài tập 3:
Đề bài: Cho hàm số sau y= -x³ + mx² – (m² + m + 1)x. Gọi S là tập hợp cho các giá trị thực của m sao cho giá trị nhỏ nhất của hàm số nằm trên đoạn [-1;1] bằng – 6. Hãy tính tổng các phần tử của S.
Lựa chọn đáp án:
- A. 0
- B. 4
- C. -5
- D. 3√2
Lời giải: