Tan(a – b) is one of the important trigonometric identities, also known as the tangent subtraction formula, used in trigonometry to find the value of the tangent trigonometric function for the difference of angles. We can find the expansion of tan(a – b) to represent the tan of a compound angle in terms of tangent trigonometric function for individual angles. Let us understand the expansion of tan(a-b) identity and its proof in detail in the following sections.
1. What is Tan(a – b) Identity in Trigonometry? 2. Tan(a – b) Compound Angle Formula 3. Proof of Tan(a – b) Identity 4. Geometrical Proof of Tan(a – b) Formula 5. How to Apply Tan(a – b)? 6. FAQs on Tan(a – b)
Tan(a-b) identity is one of the trigonometry identities for compound angles. It is applied when the angle for which the value of the tangent function is to be calculated is given in the form of the difference of any two angles. The angle (a-b) in the formula of tan(a-b) represents the compound angle.
Tan(a – b) formula for the compound angle (a-b) is referred to as the tangent subtraction formula in trigonometry. The tan(a-b) formula can be given as,
tan(a – b) = (tan a – tan b)/(1 + tan a·tan b)
We can prove the expansion of tan(a – b) given as, tan(a – b) = (tan a – tan b)/(1 + tan a·tan b) using the expansion of sin (a – b) and cos (a – b). we know, tan(a – b) = sin(a – b)/cos(a – b)
= (sin a cos b – cos a sin b)/(cos a cos b + sin a sin b)
Dividing the numerator and denominator by cos a cos b, we get
tan(a – b) = (tan a – tan b)/(1 + tan a·tan b)
Hence, proved.
We can give the proof of expansion of tan(a-b) formula using the geometrical construction method. Let us see the stepwise derivation of the formula for the tangent trigonometric function of the difference of two angles. In the geometrical proof of tan(a-b) formula, let us initially assume that ‘a’, ‘b’, and (a – b), i.e., (a > b). But this formula, in general, is true for any value of a and b.
To prove: tan (a – b) = (tan a – tan b)/(1 + tan a·tan b)
Construction: Assume a right-angled triangle PRQ with ∠PQR = a and base QR of unit length, as shown in the figure below. Take a point S on PR, such that ∠SQR = b, forming another right-angled triangle SRQ. Extend QR to point U and from this point, U, draw a perpendicular UT on PQ.
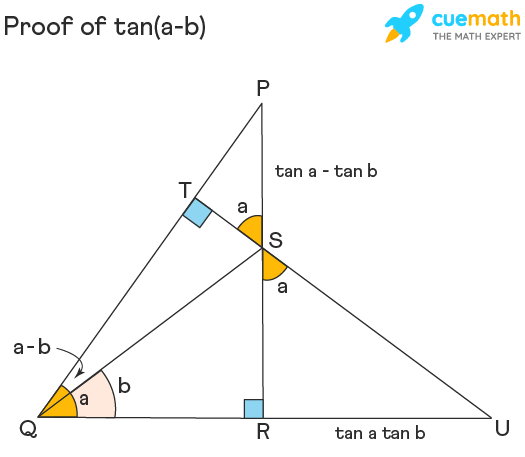
Proof: Using trigonometric formulas on the right-angled triangle PRQ we get, tan a = PR/QR ⇒ PR = QR tan a ⇒ PR = tan a (∵ QR = 1)
In right-triangle SRQ, tan b = SR/QR ⇒ SR = QR tan b ⇒ SR = tan b
⇒ PS = PR – SR = tan a – tan b
⇒ From right triangle STP, ST = cos a(tan a – tan b)
Evaluating the linear pair formed at point S and applying the angle sum property of a triangle, we get, ∠RSU = a. Also, ∠PST = a [Vertically opposite angles]
From right triangle URS, tan a = RU/SR ⇒ RU = tan a tan b
⇒ From right triangle UTQ, QT = cos a(QU) = cos a(QR + RU) = cos a(1 + tan a tan b)
Finally, in right triangle STQ,
tan(a – b) = ST/TQ = cos a(tan a – tan b)/cos a(1 + tan a tan b) = (tan a – tan b)(1 + tan a tan b)
Hence, proved.
We can apply the expansion of tan(a – b) for finding the value of the tangent trigonometric function for angles that can be represented as the difference of standard angles in trigonometry. Let us have a look at the below-given steps to learn the application of tan(a – b) identity. Take the example of tan(60º – 45º) to understand this better.
- Step 1: Compare the tan(a – b) expression with the given expression to identify the angles ‘a’ and ‘b’. Here, a = 60º and b = 45º.
- Step 2: We know, tan(a – b) = (tan a – tan b)/(1 + tan a·tan b) ⇒ tan(60º – 45º) = (tan 60º – tan 45º)/(1 + tan 60º·tan 45º) since, tan 60º = √3, tan 45º = 1 ⇒ tan(60º – 45º) = [√3 – 1]/[1 + (√3)·1] = (√3 – 1)/(√3 + 1). Also, we can compare this with the value of tan 15º = (√3 – 1)/(√3 + 1). Therefore the result is verified.
☛Related Topics on Tan(a-b):
Here are some topics that you might be interested in while reading about tan(a – b).
- sin cos tan
- Trigonometric Chart
- Trigonometric Functions
- Law of Sines
Let us have a look a few solved examples to understand tan(a-b) formula better.