Sin double angle formula in trigonometry is a sine function formula for the double angle 2θ. The formula for sin 2θ is used to simplify various problems in trigonometry. The sin double angle formula is one of the important double angle formulas in trigonometry. We can express sin of double angle formula in terms of different trigonometric functions including sin and cos, and tangent function. We know that sine of an angle is defined as the ratio of perpendicular and hypotenuse of a right-angled triangle.
In this article, we will discuss the concept of the sin double angle formula, prove its formula using trigonometric properties and identities, and understand its application. We shall solve a few examples using the different forms of the sin double angle formula for a better understanding of the concept.
1. What is Sin Double Angle Formula? 2. Sin Double Angle Formula Proof 3. Sin Double Angle Formula in Terms of Tan 4. Sin Squared Double Angle Formula 5. FAQs on Sin Double Angle Formula
Sin Double Angle Formula is a trigonometric formula that is used to simplify various expressions and problems in trigonometry. It gives the value of the sine function for the double angle 2θ, that is, sin2θ. We can express the sin double angle formula in different forms and in terms of different trigonometric functions. It is one of the primary double-angle formulas of trigonometry. Sin double angle formula can be expressed as twice the product of cosine and sine of the angle. Sin2θ formula can be expressed as:
- sin2θ = 2 sinθ cosθ
- sin2θ = 2tanθ / (1 + tan2θ)
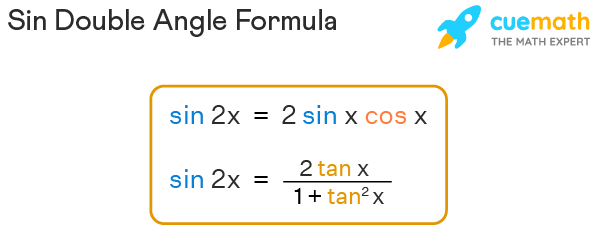
Now that we know the two sin double angle formula, let us derive these formulas using trigonometric formulas and identities. To derive the first formula of sin2θ, we will use the sin A plus B formula given by, sin (a + b) = sin a cos b + cos a sin b. In this formula, substitute a = θ and b = θ. So, we have
sin (a + b) = sin a cos b + cos a sin b
⇒ sin (θ + θ) = sin θ cos θ + cos θ sin θ
⇒ sin2θ = 2 sinθ cosθ
Hence, we have proved the first sin double angle formula.
We will use the above sin double angle formula to express in terms of tan. We will prove the sin2θ formula in terms of the tangent function. Multiply and divide the formula sin2θ = 2 sinθ cosθ by cos θ. Then, we have
sin2θ = (2 sin θ cos2θ)/(cos θ)
= 2 (sinθ / cosθ ) × (cos2θ)
We know that sin θ/cos θ = tan θ and cos θ = 1/(sec θ). So
sin2θ = 2 tan θ × (1/sec2θ)
Using one of the Pythagorean trigonometric identities, we have sec2θ = 1 + tan2θ. Substituting this, we have
sin2θ = (2tan θ)/(1 + tan2θ)
Therefore, the sin double angle formula in terms of tan is sin2θ = (2tan θ)/(1 + tan2θ).
Sin squared double angle formula gives the trigonometric formulas for the expressions sin2(2x). To express the sin2(2x) formula, we just replace θ with 2x in the sin2θ formula. So, first, let us write sin2θ formula
- sin2θ = 1 – cos2θ
- sin2θ = (1/2) (1 – cos2θ)
Now, simply replacing θ with 2x in the above formulas, we can have the sin squared double angle formulas as given below:
- sin22x = 1 – cos22x
- sin22x = (1/2) (1 – cos4x)
Important Notes on Sin Double Angle Formula
- Sin Double Angle Formula can be expressed in terms of different trigonometric functions.
- The formula for sin2θ can be expressed as:
- sin2θ = 2 sinθ cosθ
- sin2θ = 2tanθ / (1 + tan2θ)
- We can prove the sin double angle formulas using the sin (A + B) formula and other trigonometric identities.
☛ Related Topics:
- Cos Double Angle Formula
- Trigonometric Table
- Trigonometric Ratios