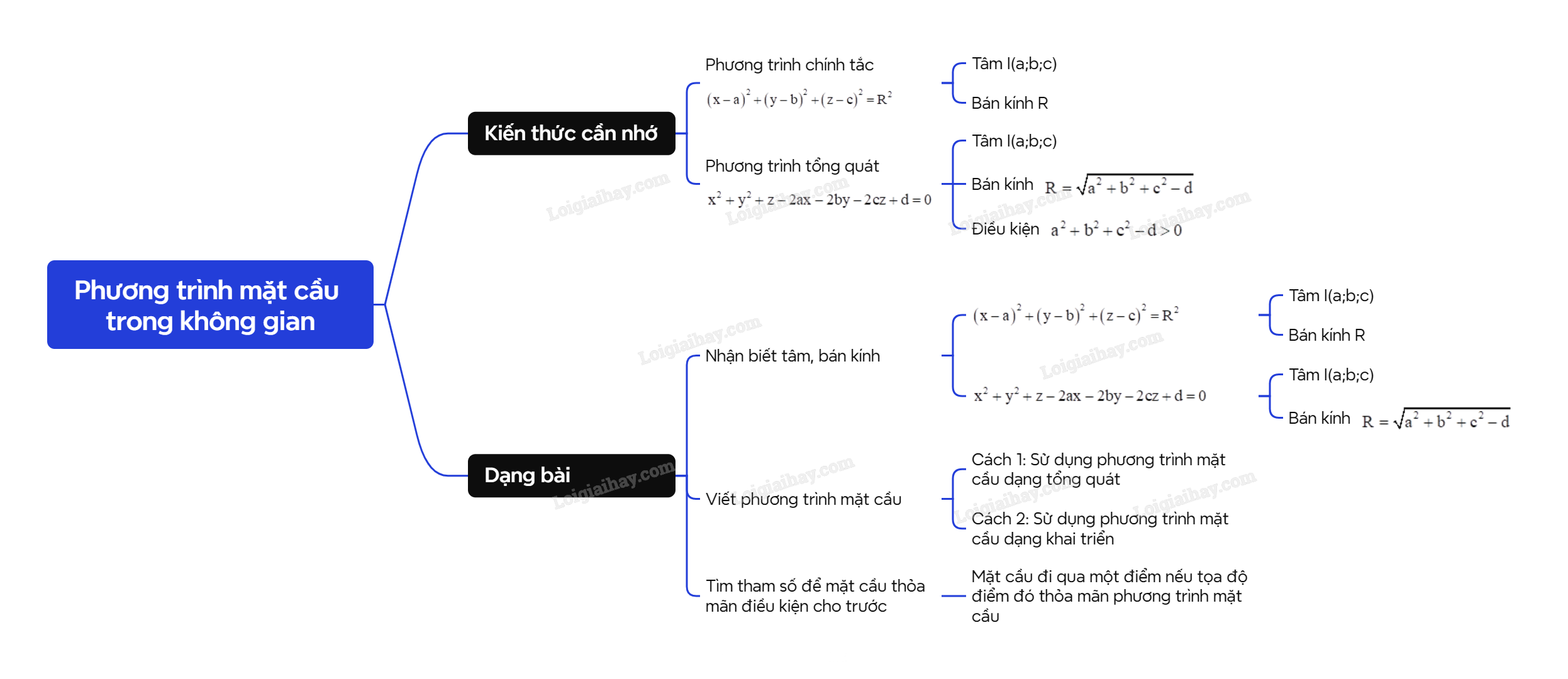
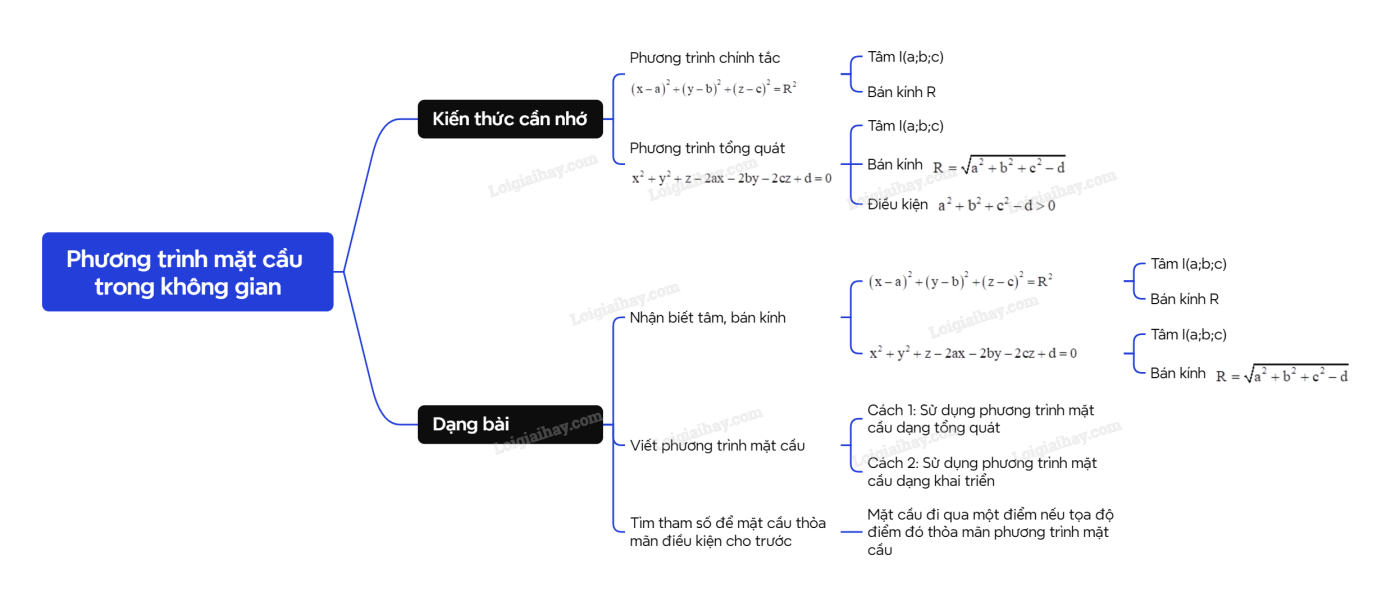
3. Bài tập về phương trình mặt cầu trong không gian
Bài 1. Trong không gian $Oxyz$ cho mặt cầu ((S):{x^2} + {y^2} + {z^2} – 2x + 4y + 2z – 3 = 0). Tính bán kính (R) của mặt cầu ((S)).
A. (R = 3)
B. (R = 9)
C. (R = sqrt 3 )
D. (R = 3sqrt 3 )
Lời giải: Phương trình có dạng ((S):{x^2} + {y^2} + {z^2} – 2ax – 2by – 2cz + d = 0) với (a = {rm{;}}1,b = – 2,c = – 1,d = {rm{;}} – 3).
Ta có công thức (R = sqrt {{a^2} + {b^2} + {c^2} – d} {rm{;}} = sqrt {{{( – 1)}^2} + {2^2} + {1^2} – ( – 3)} {rm{;}} = 3) .
Chọn đáp án A.
Bài 2. Trong không gian với hệ tọa độ Oxyz, tìm tọa độ tâm (I) và bán kính (R) của mặt cầu ({(x – 1)^2} + {(y + 2)^2} + {(z – 4)^2} = 20).
A. (Ileft( { – 1,2, – 4} right)) và (R = 5sqrt 2 )
B. (Ileft( { – 1,2, – 4} right)) và (R = 2sqrt 5 )
C. (Ileft( {1, – 2,4} right)) và (R = 20)
D. (Ileft( {1, – 2,4} right)) và (R = 2sqrt 5 )
Lời giải: Phương trình có dạng ({(x – a)^2} + {(y – b)^2} + {(z – c)^2} = {R^2}) với (a = 1,b = {rm{;}} – 2,c = 4) và (R = 2sqrt 5 ) có tâm (Ileft( {1; – 2;4} right)).
Chọn đáp án D.
Bài 3. Mặt cầu tâm (Ileft( {0;0;1} right)) bán kính (R = sqrt 2 ) có phương trình:
A. ({x^2} + {y^2} + {left( {z – 1} right)^2} = sqrt 2 )
B. ({x^2} + {y^2} + {left( {z + 1} right)^2} = sqrt 2 )
C. ({x^2} + {y^2} + {left( {z – 1} right)^2} = 2)
D. ({x^2} + {y^2} + {left( {z + 1} right)^2} = 2)
Lời giải: Mặt cầu tâm (Ileft( {0;0;1} right)) bán kính (R = sqrt 2 ) có phương trình ({x^2} + {y^2} + {left( {z – 1} right)^2} = {left( {sqrt 2 } right)^2} = 2).
Chọn đáp án C.
Bài 4. Trong không gian với hệ tọa độ $Oxyz$, tìm tập tất cả giá trị của tham số (m) để mặt cầu (left( S right)) có phương trình ({x^2} + {y^2} + {z^2} – 2x + 2my – 4z + m + 5 = 0) đi qua điểm (Aleft( {1;1;1} right)).
A. (emptyset )
B. (left{ { – frac{2}{3}} right})
C. (left{ 0 right})
D. (left{ {frac{1}{2}} right})
Lời giải: (left( S right)) có dạng ({x^2} + {y^2} + {z^2} – 2ax – 2by – 2cz + d = 0) với (a = 1,b = – m,c = 2) và (d = m + 5).
(left( S right)) là phương trình mặt cầu khi ta có ({a^2} + {b^2} + {c^2} – d > 0 Leftrightarrow 5 + {m^2} – (m + 5) > 0 Leftrightarrow {m^2} – m > 0 Leftrightarrow left[ {begin{array}{*{20}{l}}{m > 1}{m < 0}end{array}} right.)
Điểm (Aleft( {1,1,1} right)) thuộc phương trình mặt cầu (left( S right):{x^2} + {y^2} + {z^2} – 2x + 2my – 4z + m + 5 = 0) thì ta có
({1^2} + {1^2} + {1^2} – 2.1 + 2m.1 – 4.1 + m + 5 = 0 Leftrightarrow 2 + 3m = 0 Leftrightarrow m = {rm{;}} – frac{2}{3}) (thỏa mãn).
Chọn đáp án B.
Bài 5. Trong không gian với hệ tọa độ Oxyz, tìm tất cả các giá trị của (m) để phương trình ({x^2} + {y^2} + {z^2} – 2x – 2y – 4z + m = 0) là phương trình của một mặt cầu.
A. (m > 6)
B. (m ge 6)
C. (m le 6)
D. (m < 6)
Lời giải: (left( S right)) có dạng ({x^2} + {y^2} + {z^2} + 2ax + 2by + 2cz + d = 0) với (a = {rm{;}}1,b = {rm{;}}1,c = {rm{;}}2) và (d = m).
(left( S right)) là phương trình mặt cầu khi ta có ({a^2} + {b^2} + {c^2} – d > 0 Leftrightarrow 6 – m > 0 Leftrightarrow m < 6)
Chọn đáp án D.