Lời giải chi tiết
Gọi x là số lít nước cam loại A và y là số lít nước cam loại B có thể pha chế được.
– Hiển nhiên x ≥ 0 và y ≥ 0.
Để pha chế x lít nước cam loại A cần 30x gam đường, x lít nước và x gam bột cam.
Để pha chế y lít nước cam loại B cần 10y gam đường, y lít nước và 4y gam bột cam.
Tổng số đường cần dùng là: 30x + 10y (g); tổng số nước cần dùng là x + y (l) ; tổng số bột cam cần dùng là: x + 4y (gam).
– Do chỉ có 210 gam đường nên ta có bất phương trình: 30x + 10y ≤ 210, hay 3x + y ≤ 21
– Do chỉ có 9 l nước nên ta có bất phương trình: x + y ≤ 9
– Do chỉ có 24 gam bột cam nên ta có bất phương trình: x + 4y ≤ 24
Ta có hệ bất phương trình mô tả các điều kiện ràng buộc đối với x và y là:
Biểu diễn miền nghiệm của hệ bất phương trình:
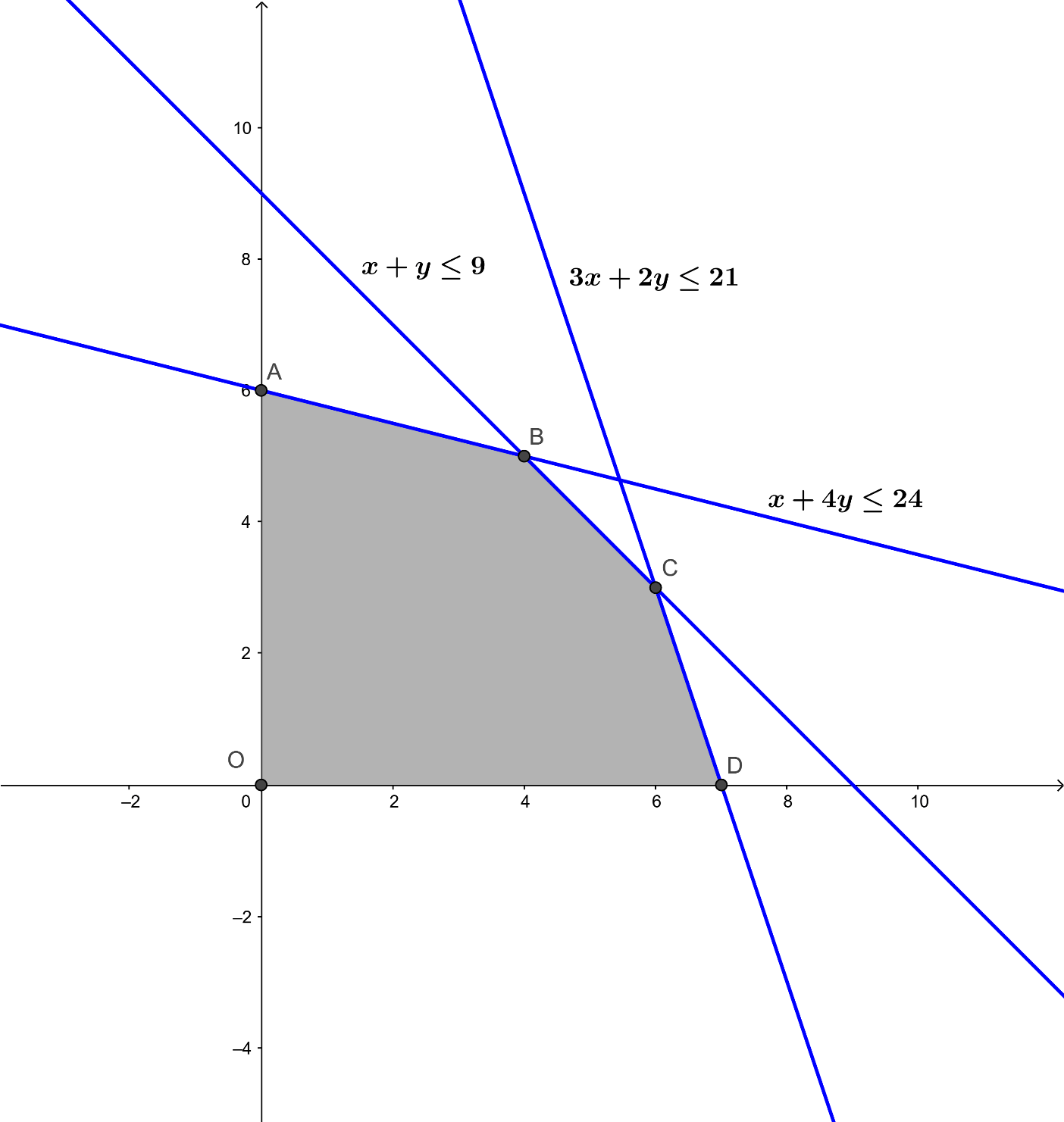
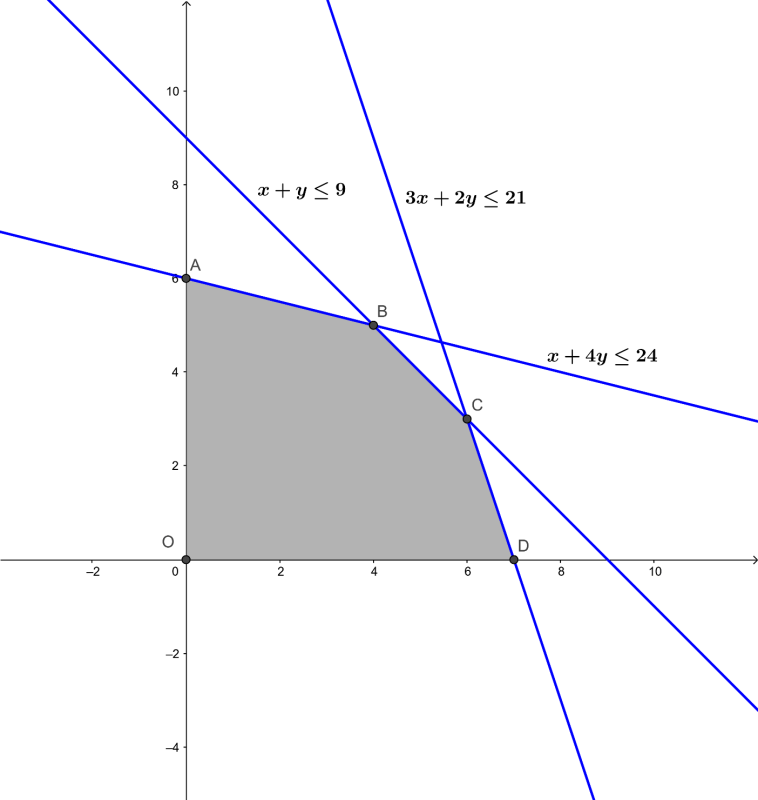
Miền nghiệm của hệ bất phương trình là miền không tô màu (ngũ giác OABCD bao gồm cả các cạnh).
Tọa độ các đỉnh của ngũ giác đó là: O(0; 0); A (0; 6); B(4; 5); C(6; 3); D (7; 0)
Gọi F là doanh thu (đơn vị: nghìn đồng) của việc bán x lít nước cam loại A và y lít nước cam loại B.
Vì mỗi lít nước cam loại A bán được 60 nghìn đồng nên x lít nước cam loại A bán được 60x (nghìn đồng). Mỗi lít nước cam loại B bán được 80 nghìn đồng nên y lít nước cam loại B bán được 80y (nghìn đồng).
Tổng số tiền thu được là 60x + 80y (nghìn đồng)
Vì vậy, ta có: T(x ; y) = 60x + 80y.
Ta phải tìm x, y thỏa mãn hệ bất phương trình sao cho T đạt giá trị lớn nhất, nghĩa là tìm giá trị lớn nhất của biểu thức T = 60x + 80y trên miền ngũ giác OABCD.
Tính các giá trị của T tại các đỉnh của ngũ giác, ta có:
Tại O(0; 0) : T = 60.0 + 80.0 = 0
Tại A(0; 6) : T = 60.0 + 80.6 = 480
Tại B(4; 5) : T = 60.4 + 80.5 = 640
Tại C(6; 3) : T = 60.6 + 80.3 = 600
Tại D(7; 0) : T = 60.7 + 80.0 = 420
T đạt giá trị lớn nhất bằng 640 tại B(4; 5).