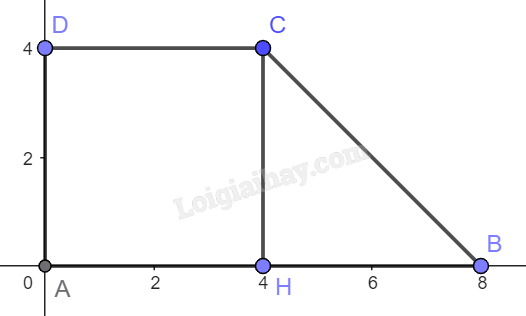
Gọi hình thang vuông ABCD như hình vẽ.
( Rightarrow {S_{ABCD}} = frac{{AD(AB + CD)}}{2} = 24).
Hình thang có đáy nhỏ là (CD = x(m)), đáy lớn là (AB = 2x(m)) với (x > 0).
( Rightarrow {S_{ABCD}} = frac{{(x + 2x)}}{2} = 24({m^2})).
( Leftrightarrow AD = frac{{48}}{{3x}} = frac{{16}}{x}(m)).
Kẻ (CH bot AB) tại (H).
Tứ giác AHCD có (widehat {CDA} = widehat {DAH} = widehat {ABC} = {90^o}).
( Rightarrow AHCD) là hình chữ nhật.
( Rightarrow left{ {begin{array}{*{20}{l}}{AH = CD = x(m)}{CH = AD = frac{{16}}{x}(m)}end{array}} right.)
( Rightarrow left{ {begin{array}{*{20}{l}}{HB = x(m)}{CH = frac{{16}}{x}(m)}end{array}} right.)
( Rightarrow BC = sqrt {C{H^2} + H{B^2}} = sqrt {{x^2} + {{left( {frac{{16}}{x}} right)}^2}} = sqrt {{x^2} + frac{{256}}{{{x^2}}}} ).
( Rightarrow P(x) = AB + BC + CD + AD)
( = 2x + sqrt {frac{{{x^4} + 256}}{{{x^2}}}} + x + frac{{16}}{x} = 3x + frac{{16}}{x} + sqrt {{x^2} + frac{{256}}{{{x^2}}}} ).
Xét (P(x) = 3x + frac{{16}}{x} + sqrt {{x^2} + frac{{256}}{{{x^2}}}} ):
(mathop {lim }limits_{x to 0} P(x) = + infty ).
( Rightarrow P(x)) có tiệm cận đứng (x = 0).
(mathop {lim }limits_{x to + infty } P(x) = + infty ).
(mathop {lim }limits_{x to – infty } P(x) = mathop {lim }limits_{x to – infty } 2x + mathop {lim }limits_{x to – infty } left( {x + frac{{16}}{x} + sqrt {{x^2} + frac{{256}}{{{x^2}}}} } right))
( = mathop {lim }limits_{x to – infty } 2x + mathop {lim }limits_{x to – infty } left( {frac{{{x^2} + frac{{256}}{{{x^2}}} + 32 – {x^2} – frac{{256}}{{{x^2}}}}}{{x + frac{{16}}{x} – sqrt {{x^2} + frac{{256}}{{{x^2}}}} }}} right))
( = mathop {lim }limits_{x to – infty } 2x + mathop {lim }limits_{x to – infty } left( {frac{{32}}{{x + frac{{16}}{x} – sqrt {{x^2} + frac{{256}}{{{x^2}}}} }}} right))
Nhận xét: (mathop {lim }limits_{x to – infty } left( {x + frac{{16}}{x} – sqrt {{x^2} + frac{{256}}{{{x^2}}}} } right) = – infty ).
( Rightarrow mathop {lim }limits_{x to – infty } P(x) = – infty ).
( Rightarrow P(x)) không có tiệm cận ngang.
Xét (P(x) – 2x = x + frac{{16}}{x} + sqrt {{x^2} + frac{{256}}{{{x^2}}}} ), ta thấy:
(mathop {lim }limits_{x to – infty } [P(x) – 2x] = mathop {lim }limits_{x to – infty } left( {x + frac{{16}}{x} + sqrt {{x^2} + frac{{256}}{{{x^2}}}} } right))
( = mathop {lim }limits_{x to – infty } frac{{{x^2} + frac{{256}}{{{x^2}}} + 32 – {x^2} – frac{{256}}{{{x^2}}}}}{{x + frac{{16}}{x} – sqrt {{x^2} + frac{{256}}{{{x^2}}}} }})
( = mathop {lim }limits_{x to – infty } frac{{32}}{{x + frac{{16}}{x} – sqrt {{x^2} + frac{{256}}{{{x^2}}}} }} = 0).
( Rightarrow y = 2x) là 1 tiệm cận xiên của (P(x)).
Xét (P(x) – 4x = frac{{16}}{x} – x + sqrt {{x^2} + frac{{256}}{{{x^2}}}} ), ta thấy:
(mathop {lim }limits_{x to + infty } [P(x) – 4x] = mathop {lim }limits_{x to + infty } left( {frac{{16}}{x} – x + sqrt {{x^2} + frac{{256}}{{{x^2}}}} } right))
( = mathop {lim }limits_{x to + infty } frac{{{x^2} + frac{{256}}{{{x^2}}} – 32 – {x^2} – frac{{256}}{{{x^2}}}}}{{frac{{16}}{x} – x – sqrt {{x^2} + frac{{256}}{{{x^2}}}} }})
( = mathop {lim }limits_{x to + infty } frac{{ – 32}}{{frac{{16}}{x} – x – sqrt {{x^2} + frac{{256}}{{{x^2}}}} }}).
Nhận xét: (mathop {lim }limits_{x to + infty } left( {frac{{16}}{x} – x – sqrt {{x^2} + frac{{256}}{{{x^2}}}} } right) = – infty ).
( Rightarrow mathop {lim }limits_{x to – infty } frac{{ – 32}}{{frac{{16}}{x} – x – sqrt {{x^2} + frac{{256}}{{{x^2}}}} }} = 0).
( Rightarrow y = 4x) là 1 tiệm cận xiên của (P(x)).
( Rightarrow P(x)) có 3 tiệm cận, gồm 1 tiệm cận đứng (x = 0) và 2 tiệm cận xiên (y = 2x) và (y = 4x).
Nguồn: Hoidap247.
