Giới thiệu về góc kề nhau và góc bù nhau

Góc kề nhau và góc bù nhau là hai khái niệm thường xuất hiện trong hình học cấp 2. Phần dưới đây sẽ giúp bạn hiểu rõ định nghĩa, tính chất của hai loại góc này:
Góc kề nhau
Góc kề nhau là hai góc có các đặc điểm sau:
– Có một đỉnh chung.
– Có một cạnh chung.
– Hai cạnh còn lại nằm ở hai phía đối nhau so với cạnh chung.
Khi biểu diễn trên hình, hai góc kề nhau thường được đặt liền nhau, chung một đỉnh và một cạnh, còn hai cạnh còn lại mở ra về hai phía, tạo thành hai phần không trùng nhau của mặt phẳng.
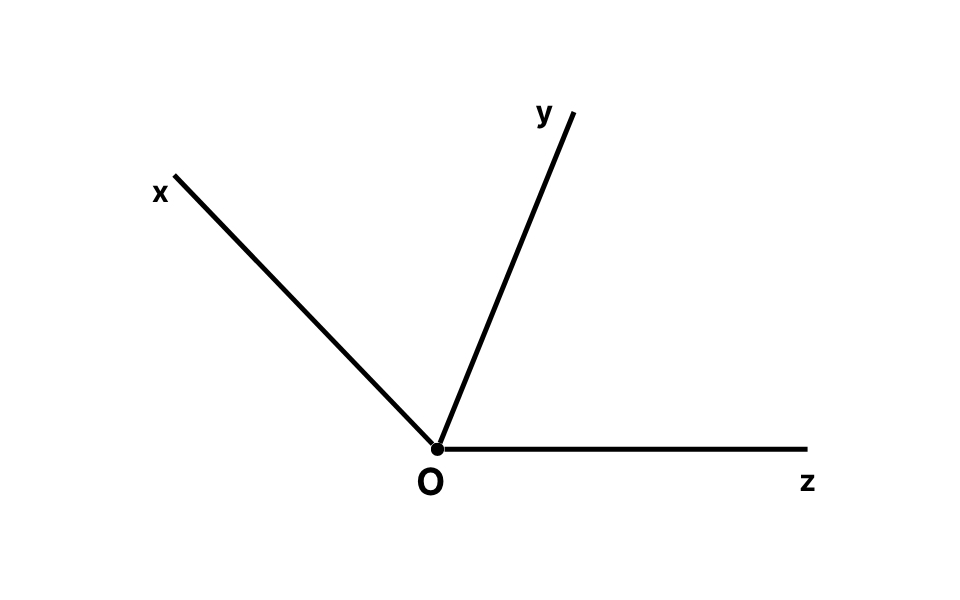
Ví dụ: Nếu hai góc ∠xOy và ∠yOz có đỉnh O chung và cạnh Oy chung, đồng thời Ox và Oz nằm ở hai phía đối với tia Oy thì chúng là hai góc kề nhau.
Tính chất của góc kề nhau
Góc kề nhau có một số tính chất hình học như sau:
– Hai góc kề nhau có thể có tổng bằng bất kỳ giá trị nào, không cố định là 90° hay 180°.
– Khi hai góc kề nhau có tổng bằng 180°, chúng được gọi là góc kề bù.
– Nếu hai góc kề nhau có tổng bằng 90°, chúng được gọi là góc kề vuông.
Như vậy, góc kề nhau chỉ thể hiện mối quan hệ về vị trí giữa hai góc, không quy định về tổng số đo của chúng.
Góc bù nhau
Góc bù nhau là hai góc có tổng số đo bằng 180 độ, không yêu cầu phải nằm cạnh nhau hay có chung đỉnh.
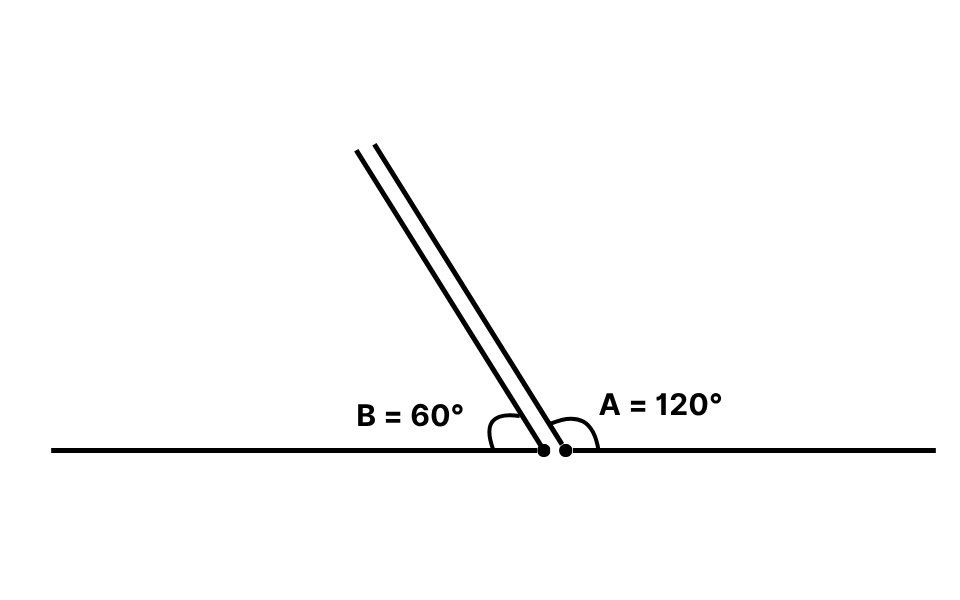
Ví dụ: Nếu góc A = 120° và góc B = 60°, thì A và B là hai góc bù nhau vì 120 + 60 = 180.
Tính chất của góc bù nhau
Góc bù nhau có các đặc điểm như sau:
– Tổng số đo của hai góc luôn bằng 180 độ.
– Hai góc bù nhau không cần thiết phải kề nhau, tức là chúng có thể nằm cách xa nhau trong hình hoặc không chung cạnh nào.
– Nếu hai góc bù nhau lại có thêm một cạnh chung và nằm liền nhau, thì chúng chính là góc kề bù.
Từ tính chất trên, góc bù nhau thường được sử dụng trong các bài toán tính toán góc hoặc chứng minh hình học, đặc biệt trong các trường hợp liên quan đến đường thẳng và góc bẹt.
Góc kề bù là gì?

Góc kề bù là một khái niệm cơ bản trong chương trình Toán hình học lớp 7. Hai góc được gọi là kề bù khi chúng cùng thỏa mãn các điều kiện sau:
– Có một đỉnh chung.
– Có một cạnh chung.
– Hai cạnh còn lại là hai tia đối nhau, nghĩa là chúng nằm trên cùng một đường thẳng nhưng hướng ngược chiều.
Nói cách khác, hai góc kề bù là hai góc vừa kề nhau, tức là đặt cạnh nhau, vừa bù nhau, tức là tổng số đo bằng 180 độ.
Một ví dụ dễ hình dung: nếu có hai góc là xOy và yOz, trong đó điểm O là đỉnh chung, tia Oy là cạnh chung, còn hai tia Ox và Oz là hai tia đối nhau thì hai góc xOy và yOz là hai góc kề bù.
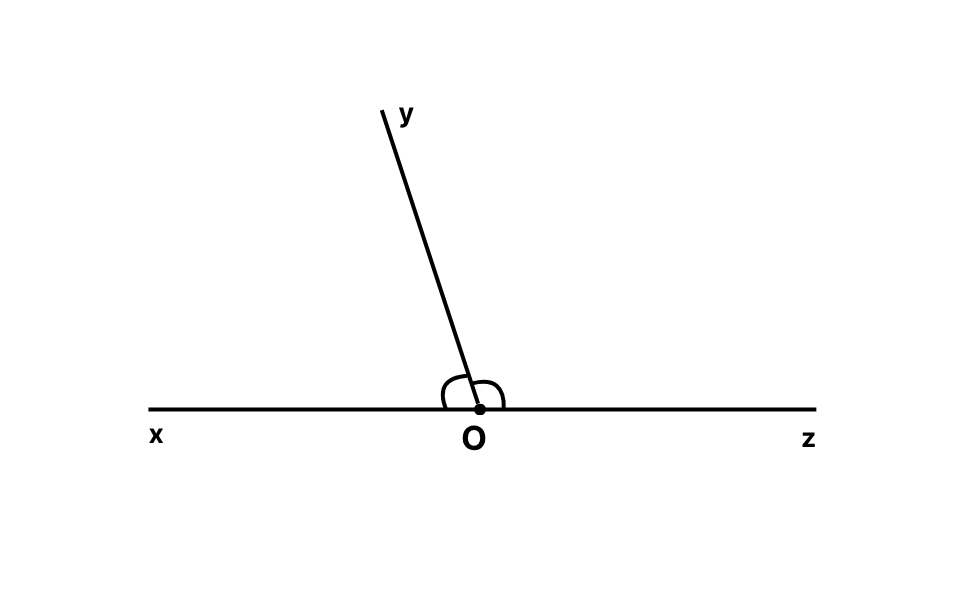
Khi nhìn trên hình vẽ, bạn sẽ thấy hai góc này nằm liền nhau, cùng chia sẻ một tia chung ở giữa, và phần còn lại tạo thành một đường thẳng kéo dài về hai phía.
Các tính chất nổi bật của góc kề bù
Tính chất vừa kề vừa bù
Góc kề bù là sự kết hợp của hai yếu tố hình học cơ bản: kề nhau và bù nhau. Để hiểu rõ bản chất của góc kề bù, cần nắm vững từng khái niệm riêng lẻ như sau:
– Góc kề nhau là hai góc có một đỉnh chung, một cạnh chung, và hai cạnh còn lại nằm ở hai phía khác nhau so với cạnh chung.
– Góc bù nhau là hai góc có tổng số đo bằng 180 độ, nhưng không cần phải đặt cạnh nhau hay có chung đỉnh.
Tính chất hình học: Tạo thành một đường thẳng
Một đặc điểm quan trọng khác của góc kề bù là: hai cạnh không chung của chúng là hai tia đối nhau, tức là nằm trên một đường thẳng kéo dài về hai phía. Khi hai góc kề bù được ghép lại, chúng tạo nên một góc bẹt có số đo đúng bằng 180 độ.
Tính chất đặc trưng của hai góc kề bù khi tổng số đo luôn bằng 180 độ là dấu hiệu quan trọng để nhận biết và phân biệt góc kề bù với các loại góc khác.
Khi hai góc kề bù được ghép lại, chúng tạo thành một góc bẹt, tức là một góc có số đo đúng bằng 180 độ và nằm trên một đường thẳng.
Công thức tổng quát biểu diễn mối quan hệ này như sau:
Nếu A và B là hai góc kề bù thì: A + B = 180°
Ví dụ: nếu góc A có số đo là 70 độ, thì góc kề bù với nó sẽ là 110 độ. Khi cộng lại, ta được 70 + 110 = 180, đúng với định nghĩa của góc kề bù.
Dưới đây là bảng tổng hợp của 3 loại góc:
Tiêu chí
Góc kề nhau
Góc bù nhau
Góc kề bù
Chung đỉnh
Có
Không bắt buộc
Có
Chung cạnh
Có
Không có
Có
Hai cạnh còn lại
Nằm ở hai phía đối với cạnh chung
Không yêu cầu vị trí
Là hai tia đối nhau
Tổng số đo
Không cố định
Bằng 180 độ
Bằng 180 độ
Tạo thành đường thẳng
Không
Không
Có (tạo thành góc bẹt)
Quan hệ vị trí
Hai góc liền nhau
Có thể không liền nhau
Hai góc liền nhau
Bài tập góc kề bù

Dưới đây là những dạng bài tập từ cơ bản đến nâng cao về góc kề bù bạn có thể tham khảo:
Bài tập dạng cơ bản
Bài 1: Cho ba tia Ox, Oy, Oz cùng xuất phát từ điểm O. Biết tia Oy nằm giữa hai tia Ox và Oz. Góc xOy có số đo là 45°, góc yOz có số đo là 35°.Hỏi: Hai góc xOy và yOz có phải là hai góc kề nhau không? Tính số đo góc xOz.
Đáp án:Vì Oy nằm giữa Ox và Oz, nên xOy và yOz có:- Chung đỉnh O- Chung cạnh Oy- Hai cạnh còn lại (Ox và Oz) nằm về hai phía đối với Oy=> Vậy ∠xOy và ∠yOz là hai góc kề nhau.Tính góc xOz:∠xOz = ∠xOy + ∠yOz = 45° + 35° = 80°
Bài 2: Hai góc A và B có tổng số đo bằng 180 độ. Biết góc A = 112°.Tính số đo góc B và cho biết A và B có phải là hai góc bù nhau không?
Đáp án:Vì A + B = 180° và A = 112°, nên:B = 180° – 112° = 68°Do tổng bằng 180°, nên A và B là hai góc bù nhau.
Bài 3: Hai góc xOy và yOz là hai góc kề bù. Biết số đo của góc yOz là 65°.Hỏi: Số đo của góc xOy là bao nhiêu?
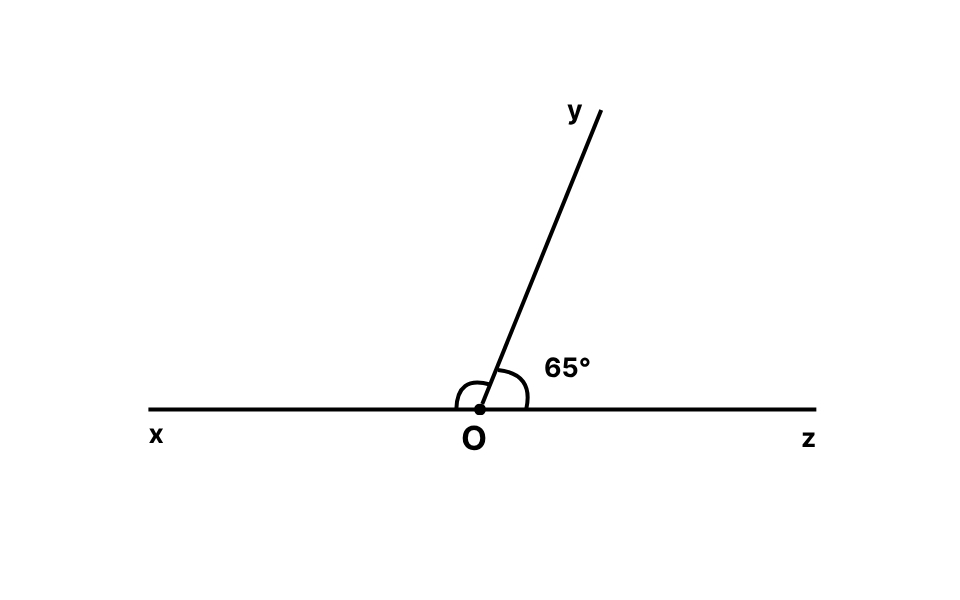
Đáp án:Tổng hai góc kề bù bằng 180°, nên:xOy = 180° – 65° = 115°
Bài 4: Cho hai góc A và B là hai góc kề bù. Biết góc A = 100°.Tính số đo góc B.
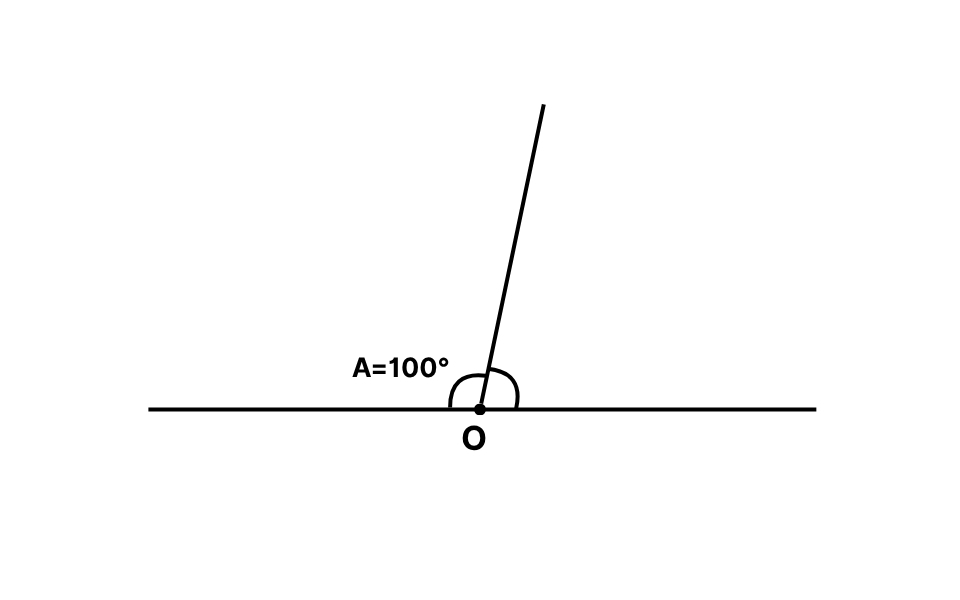
Đáp án:A + B = 180° ⇒ B = 180° – 100° = 80°
Bài 5: Góc xOy và yOz là hai góc kề nhau. Biết xOy = 90° và tổng hai góc là 180°.Hỏi: Hai góc này có phải là góc kề bù không?
Đáp án:Vì xOy và yOz có chung một cạnh và tổng bằng 180° nên xOy và yOz là hai góc kề bù.
Bài tập dạng nâng cao
Bài 6: Hai góc A và B là hai góc kề bù, biết:A = 2x + 10, B = 6x – 46.Tìm giá trị của x và số đo mỗi góc.
Đáp án:A + B = 180°(2x + 10) + (6x – 46) = 1808x – 36 = 1808x = 216 ⇒ x = 27A = 2×27 + 10 = 64°B = 6×27 – 46 = 116°
Bài 7: Cho ba tia Ox, Oy, Oz sao cho tia Oy nằm giữa Ox và Oz. Biết:∠xOy = 3x + 15, ∠yOz = 5x – 5.Tính số đo mỗi góc nếu xOy và yOz là hai góc kề bù.
Đáp án:Vì hai góc kề bù:(3x + 15) + (5x – 5) = 1808x + 10 = 1808x = 170 ⇒ x = 21.25xOy = 3×21.25 + 15 = 78.75°yOz = 5×21.25 – 5 = 101.25°
Kết luận
Nắm vững khái niệm các loại góc kề nhau, góc bù nhau và góc kề bù sẽ giúp học sinh tự tin giải quyết các bài toán lớp 7 về góc và cũng để học tốt các phần kiến thức liên quan đến đường thẳng, tia và quan hệ giữa các yếu tố hình học. Trung tâm gia sư online Học là Giỏi hy vọng bài viết đã giúp bạn hiểu rõ hơn về kiến thức liên quan đến các loại góc trên một cách dễ dàng và chính xác.
