In trigonometry, cos(a – b) is one of the important trigonometric identities, that finds application in finding the value of the cosine trigonometric function for the difference of angles. The expansion of cos (a – b) helps in representing the cos of a compound angle in terms of trigonometric functions sine and cosine. Let us understand the cos(a-b) identity and its proof in detail in the following sections.
1. What is Cos(a – b) Identity in Trigonometry? 2. Cos(a – b) Compound Angle Formula 3. Proof of Cos(a – b) Formula 4. How to Apply Cos(a – b)? 5. FAQs on Cos(a – b)
Cos (a – b) is the trigonometric identity for compound angles. We apply the cos (a-b) identity formula when the angle for which the value of the cosine function is to be calculated is given in the form of the difference of angles. The angle (a-b) represents the compound angle.
We refer to cos(a – b) formula as the subtraction formula in trigonometry. The cos(a – b) formula for the compound angle (a-b) can be given as,
cos (a – b) = cos a cos b + sin a sin b
The proof of expansion of cos(a-b) formula can be given using the geometrical construction method. Let us see the stepwise derivation of the formula for the cosine trigonometric function of the difference of two angles. In the geometrical proof of cos(a-b) formula, we initially assume that ‘a’ and ‘b’ are positive acute angles, such that angle a > angle b. This formula, in general, is true for any positive or negative value of a and b.
To prove: cos (a – b) = cos a cos b + sin a sin b
Construction: Draw a line OX in a plane and let us rotate it about O in the anti-clockwise direction to a point Z, making an acute ∠XOZ = a, from starting position to its final position. Again, rotate the line, this time in the backward direction, starting from the position OZ till it reaches a point Y, thus making out an acute angle given as, ∠ZOY = b. Therefore, ∠XOY = a – b.
Next, take a point P on OY, and draw PQ and PR perpendiculars to OX and OZ respectively. Draw perpendiculars RS and RT from point R upon OX and PQ respectively.
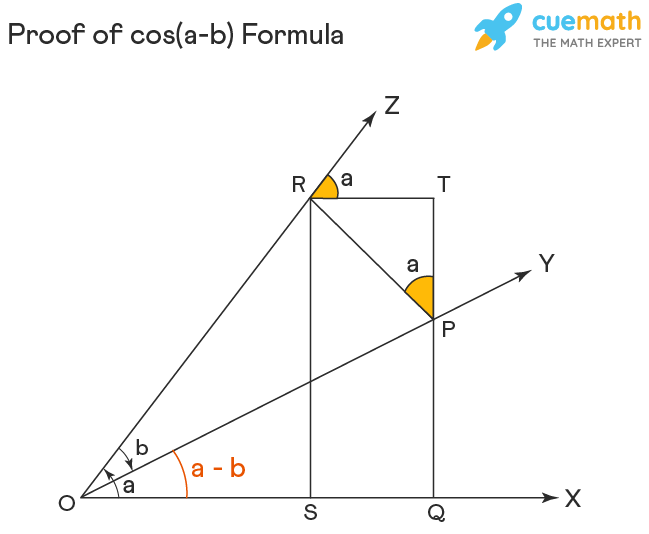
Now, from the right-angled triangle PQO we get, cos (a – b) = OQ/OP = (OS+SQ)/OP = OS/OP + SQ/OP = OS/OP + TR/OP = OS/OR ∙ OR/OP + TR/PR ∙ PR/OP = cos a cos b + sin ∠TPR sin b = cos a cos b + sin a sin b, (since we know, ∠TPR = a)
Therefore, cos (a – b) = cos a cos b + sin a sin b.
The expansion of cos(a – b) can be used to find the value of the cosine trigonometric function for angles that can be represented as the difference of standard angles in trigonometry. We can follow the steps given below to learn to apply cos(a – b) identity. Let us evaluate cos(90º – 30º) to understand this better.
- Step 1: Compare the cos(a – b) expression with the given expression to identify the angles ‘a’ and ‘b’. Here, a = 90º and b = 30º.
- Step 2: We know, cos (a – b) = cos a cos b + sin a sin b. ⇒ cos(90º – 30º) = cos 90ºcos 30º + sin 90ºsin 30º since, sin 90º = 1, sin 30º = 1/2, cos 90º = 0, cos 30º = √3/2 ⇒ cos(90º – 30º) = (0)(√3/2) + (1)(1/2) = 0 + 1/2 = 1/2 Also, we know that cos 60º = 1/2. Therefore the result is verified.
Let us have a look a few solved examples to understand cos(a-b) formula better.