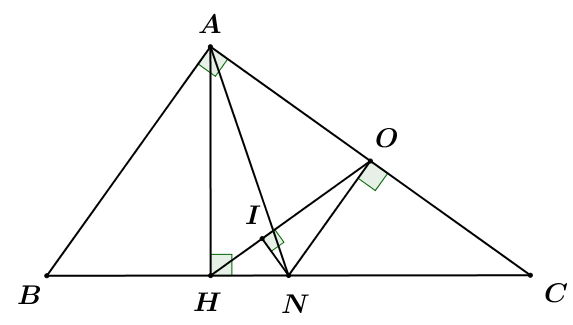
a) Chứng minh AONH là tứ giác nội tiếp.
Xét tứ giác AONH có:
(begin{array}{l}angle AHN = {90^0},,left( {do,,AH bot BC} right)angle AON = {90^0},,left( {do,,NO bot AC} right)end{array})
( Rightarrow angle AHN + angle AON = {90^0} + {90^0} = {180^0}).
Mà H, O là hai đỉnh kề nhau của tứ giác AONH nên AONH là tứ giác nội tiếp (dhnb).
b) Chứng minh CO.CA = CN.CH.
Xét (Delta CON) và (Delta CHA) có:
(begin{array}{l}angle ACH,,chungangle CON = angle CHA,,left( { = {{90}^0}} right) Rightarrow Delta CON sim Delta CHA,,left( {g.g} right)end{array})
( Rightarrow dfrac{{CO}}{{CH}} = dfrac{{CN}}{{CA}}) (cặp cạnh tương ứng tỉ lệ).
( Rightarrow CO.CA = CN.CH,,left( {dpcm} right))
c) Tính độ dài đường cao NI của tam giác NHO.
Kẻ (NI bot OH) tại I.
Xét (Delta OIN) và (Delta AHN) có:
(angle NOI = angle NAH) (hai góc nội tiếp cùng chắn cung HN của tứ giác nội tiếp AONH).
(begin{array}{l}angle OIN = angle AHN,,left( { = {{90}^0}} right) Rightarrow Delta OIN sim Delta AHN,,left( {g.g} right)end{array})
( Rightarrow dfrac{{NI}}{{HN}} = dfrac{{ON}}{{AN}}) (cặp cạnh tương ứng tỉ lệ) ( Rightarrow NI = dfrac{{ON.HN}}{{AN}},,left( * right)).
Ta có: N là trung điểm của BC (gt)
(left{ begin{array}{l}AB bot ACON bot ACend{array} right. Rightarrow ONparallel AB) (từ vuông góc đến song song)
( Rightarrow O) là trung điểm của AC (định lí đường trung bình của tam giác).
=> ON là đường trung bình của tam giác ABC.
( Rightarrow ON = dfrac{1}{2}AB = dfrac{1}{2}.6 = 3,,left( {cm} right)).
Xét tam giác vuông ABC, đường cao AH:
+) Áp dụng định lí Pytago: (B{C^2} = A{B^2} + A{C^2} = {6^2} + {8^2} = 100) ( Rightarrow BC = 10,,left( {cm} right)).
( Rightarrow BN = dfrac{1}{2}BC = dfrac{1}{2}.10 = 5,,left( {cm} right))
+) AN là đường trung tuyến ứng với cạnh huyền BC ( Rightarrow AN = dfrac{1}{2}BC = dfrac{1}{2}.10 = 5,,left( {cm} right))
+) Áp dụng hệ thức lượng: (A{B^2} = BH.BC Rightarrow BH = dfrac{{A{B^2}}}{{BC}} = dfrac{{{6^2}}}{{10}} = 3,6,,left( {cm} right)).
( Rightarrow HN = BN – BH = 5 – 3,6 = 1,4,,left( {cm} right)).
Thay độ dài ON, HN, AN vào (*) ta có: (NI = dfrac{{ON.HN}}{{AN}} = dfrac{{3.1,4}}{5} = 0,84,,left( {cm} right)).
Vậy độ dài đường cao NI của tam giác NHO là NI = 0,84 (cm).
