Hướng dẫn giải
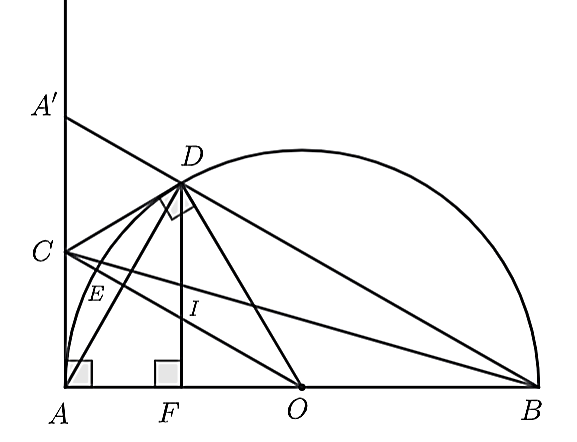
a) Xét (Delta CAO) vuông tại (A) ((CA) là tiếp tuyến) nên ba điểm (O,A,C) cùng thuộc đường tròn đường kính (CO.) (1)
Xét (Delta CDO) vuông tại (D) ((DC) là tiếp tuyến) nên ba điểm (O,C,D) cùng thuộc đường tròn đường kính (CO.) (2)
Từ (1) và (2) suy ra bốn điểm (O,A,C,D) cùng thuộc một đường tròn đường kính (CO.)
b) Gọi (BD) cắt (AC) tại (A’), (BC) cắt (DF) tại (I).
Xét (Delta ADB) có trung tuyến (OD = frac{1}{2}AB) nên (Delta ADB) vuông tại (D).
Suy ra (Delta ADA’) vuông tại (D).
Lại có (CD = CA) (tính chất hai tiếp tuyến cắt nhau) nên suy ra được [CD = AC’].
Suy ra [Delta CAD] cân tại [C] nên [widehat {CAD} = widehat {CDA}].
Có [widehat {CAD} + widehat {AA’D} = widehat {CDA} + widehat {CDA’} = 90^circ ] nên [widehat {AA’D} = widehat {A’DC}].
Suy ra (CA’ = A’D).
Từ đây suy ra (CA’ = CA = CD) hay (C) là trung điểm của (AA’).
Mặt khác, (DFparallel AA ‘) (cùng vuông góc với (AB)) nên theo định lí Thalès thì (frac{{ID}}{{CA’}} = frac{{IF}}{{CA}}left( { = frac{{BI}}{{BC}}} right)) (2)
Từ (1) và (2) suy ra (ID = IF).
Do đó, (BC) đi qua trung điểm của (DF.)
c) Ta có: (cos widehat {COD} = frac{{OD}}{{OC}} = frac{R}{{2R}} = frac{1}{2}) suy ra (widehat {COD} = 60^circ .)
Suy ra (widehat {AOD} = 180^circ – widehat {COD} = 180^circ – 60^circ = 120^circ ).
Ta có ({S_{quat{rm{ }}AOD}} = frac{{pi cdot {R^2} cdot 120^circ }}{{360^circ }} = frac{{pi {R^2}}}{3}).
Áp dụng định lí Pythagore vào tam giác (COD), có (CD = sqrt {C{O^2} – O{D^2}} = sqrt {4{R^2} – {R^2}} = Rsqrt 3 ).
Ta có: ({S_{OCD}} = frac{1}{2}CD cdot DO = frac{1}{2} cdot Rsqrt 3 cdot R = frac{{{R^2}sqrt 3 }}{2}).
Xét (Delta DCO) và (Delta ACO), có: (CO) chung (gt)
(CA = CD) (tính chất)
(OA = OD = R) (gt)
Do đó, (Delta DCO = Delta ACO) (c.c.c).
Suy ra ({S_{ACO}} = {S_{COD}} = frac{1}{2}{S_{ACDO}}).
Do đó, ({S_{ACDO}} = 2{S_{CDO}} = {R^2}sqrt 3 ).
Diện tích phần tam giác (ACD) nằm ngoài đường tròn là: ({R^2}sqrt 3 – frac{{pi {R^2}}}{3} = left( {sqrt 3 – frac{pi }{3}} right){R^2}).
