Hướng dẫn giải
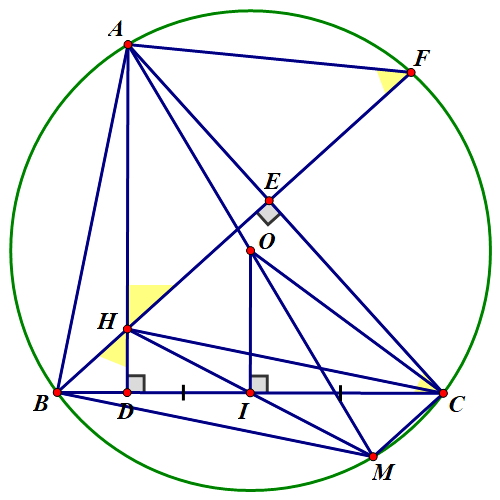0 ) và dây cung B C cố định. Một điểm A chuyển động trên cung lớn B C sao cho tam giác A B C có ba góc nhọn. Kẻ các đường cao A D , B E của tam giác A B C cắt nhau tại H và B E cắt đường tròn ( O ) tại F ( F khác B ) . (ảnh 1)” width=”273″ height=”273″ />
a) Gọi (O’) là trung điểm của cạnh [CH.]
Ta có (HD bot CD) nên (widehat {HDC} = 90^circ ).
Xét (Delta HDC)vuông tại [D] có (DO’) là trung tuyến nên (DO’ = HO’ = CO’ = frac{1}{2}HC).
Chứng ming tương tự, ta có (CO’ = HO’ = EO’ = frac{1}{2}HC).
Do đó (DO’ = HO’ = CO’ = EO’ = frac{1}{2}HC).
Vậy bốn điểm (D,,,H,,,E,,,C) cùng thuộc một đường tròn.
Vậy tứ giác (DHEC) nội tiếp đường tròn.
b) Trong tam giác (ABC) có (BE,,,AD) là hai đường cao cắt nhau tại (H).
Vì (H) là trực tâm tam giác (ABC) nên (CH bot AB).
Trong(left( O right)) có (widehat {ABM},,,widehat {ACM}) là hai góc nội tiếp cùng chắn nửa đường tròn đường kính (AM).
Suy ra (widehat {ABM} = widehat {ACM} = 90^circ ) nên (MB bot AB,;,,MC bot AC.)
Mà (CH bot AB,;,,BH bot AC) nên (MB,{rm{//}},CH,,,MC,{rm{//}},BH) nên (BHCM) là hình bình hành.
Xét đường tròn (left( O right)) có (OI bot BC) tại (I) nên (I) là trung điểm của (BC) (đường kính vuông góc với dây).
c) Xét (Delta DHB) và (Delta DCA) có
(widehat {BDH} = widehat {ADC} = 90^circ ) (vì (AD bot BC))
(widehat {HBD} = widehat {DAC}) (cùng phụ (widehat {ACB}))
Do đó .
Suy ra (frac{{DH}}{{DC}} = frac{{DB}}{{DA}}) hay (DH cdot DA = DB cdot DC.)
Ta có ({left( {a – b} right)^2} ge 0) hay ({a^2} – 2ab + {b^2} ge 0) nên ({a^2} + 2ab + {b^2} ge 4ab), suy ra (ab le frac{{{{left( {a + b} right)}^2}}}{4}).
Áp dụng bất đẳng thức (ab le frac{{{{left( {a + b} right)}^2}}}{4}), ta có: (DB cdot DC le frac{{{{left( {DB + DC} right)}^2}}}{4} = frac{{B{C^2}}}{4}).
Suy ra (DH cdot DA le frac{{B{C^2}}}{4}) không đổi vì (BC) cố định.
Dấu xảy ra khi (DB = DC), khi đó (A) là điểm chính giữa cung lớn .
Vậy (A) là điểm chính giữa cung lớn thì giá trị lớn nhất của (DH cdot DA) bằng (frac{{B{C^2}}}{4}).