Lời giải
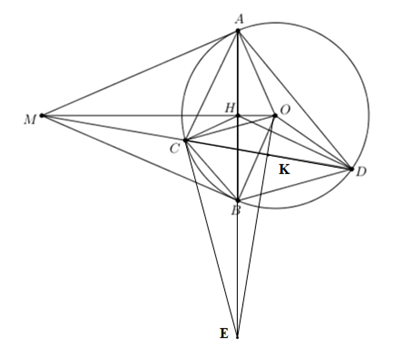
a) Vì MA, MB là tiếp tuyến của (O) cắt nhau tại M
Nên MA ⊥ OA, MB ⊥ OB, MA = MB
Suy ra (widehat {OAM} = widehat {OBM} = 90^circ )
Xét tứ giác AMBO có (widehat {OAM} + widehat {OBM} = 90^circ + 90^circ = 180^circ )
Suy ra tứ giác AMBO nội tiếp
Vậy tứ giác AMBO nội tiếp .
b) Xét (O) có (widehat {CBM}) là góc tạo bởi tiếp tuyến và dây cung BC
(widehat {B{rm{D}}M}) là góc nội tiếp chắn cung BC
Suy ra (widehat {CBM} = widehat {MDB})
Xét tam giác MBC và tam giác MDB có
(widehat {CBM} = widehat {MDB})
(widehat {BMD}) là góc chung
Suy ra (g.g)
Do đó (frac{{{rm{MB}}}}{{{rm{MD}}}} = frac{{{rm{MC}}}}{{{rm{MB}}}})
Suy ra MC . MD = MB2
Mà MA = MB (chứng minh câu a)
Suy ra MC . MD = MA2 (1)
Vì MA = MB nên M thuộc trung trực của AB
Vì OA = OB nên O thuộc trung trực của AB
Suy ra MO là trung trực của AB
Do đó MO ⊥ AB
Xét tam giác MAO vuông tại A có MO ⊥ AH
Suy ra MH . MO = MA2 (hệ thức lượng trong tam giác vuông) (2)
Từ (1) và (2) suy ra MC . MD = MH . MO
c) Vì MC . MD = MH . MO nên (frac{{MC}}{{MO}} = frac{{MH}}{{M{rm{D}}}})
Xét tam giác MCH và tam giác MOD có
(widehat {OMD}) là góc chung
(frac{{MC}}{{MO}} = frac{{MH}}{{M{rm{D}}}}) (chứng minh trên)
Suy ra (c.g.c)
Do đó (widehat {MHC} = widehat {MDO}) (hai góc tương ứng)
Mà (widehat {MHC} + widehat {OHC} = 180^circ )
Suy ra (widehat {MDO} + widehat {OHC} = 180^circ )
Do đó tứ giác CHOD nội tiếp
Suy ra (widehat {OH{rm{D}}} = widehat {OC{rm{D}}})
Vì OC = OD nên tam giác OCD cân tại O
Suy ra (widehat {O{rm{DC}}} = widehat {OC{rm{D}}})
Mà (widehat {OH{rm{D}}} = widehat {OC{rm{D}}}) nên (widehat {O{rm{DC}}} = widehat {OH{rm{D}}})
Lại có (widehat {MHC} = widehat {CDO}) (chứng minh trên)
Suy ra (widehat {MHC} = widehat {OH{rm{D}}})
Suy ra (90^circ – widehat {MHC} = 90^circ – widehat {OH{rm{D}}})
Hay (widehat {BHC} = widehat {BH{rm{D}}})
Mà (widehat {BHC} + widehat {BH{rm{D}}} = widehat {CH{rm{D}}})
Suy ra (frac{{widehat {CH{rm{D}}}}}{2} = widehat {CHB})
Xét tam giác COD cân tại O có OK là trung tuyến
Suy ra OK là phân giác của góc COD
Do đó (frac{{widehat {{rm{COD}}}}}{2} = widehat {{rm{COK}}})
Xét (O) có (widehat {CH{rm{D}}},widehat {{rm{ COD}}})cùng chắn cung CD
Suy ra (widehat {CH{rm{D}}} = widehat {{rm{COD}}})
Suy ra (frac{{widehat {CH{rm{D}}}}}{2} = frac{{widehat {{rm{COD}}}}}{2})
Do đó (widehat {CHB} = widehat {{rm{COE}}})
Xét tứ giác CHOE có (widehat {CHE} = widehat {{rm{COE}}})
(widehat {CHE},widehat {{rm{COE}}}) cùng chắn cung CE
Suy ra tứ giác CHOE nội tiếp
Suy ra (widehat {OHE} = widehat {{rm{OCE}}}) (vì cùng chắn cung OE)
Mà (widehat {OHE} = {rm{90}}^circ )
Nên (widehat {OCE} = {rm{90}}^circ )
Hay OC ⊥ CE
Xét (O) có OC ⊥ CE, OC là bán kính
Suy ra EC là tiếp tuyến của (O)
Vậy EC là tiếp tuyến của (O).
